해당 글은 3Blue1Brown 채널의 Essence of linear algebra를 정리한 스터디 노트입니다.

Chapter 6. Essence of linear algebra

선형 변환을 다루다 보면, 공간을 확대시키는 Stretches 변환이나 축소시키는 squishes 변환을 볼 수 있습니다. 이러한 변환을 이해하는 방법 중 하나로 바로 물체가 얼마나 확장되거나 축소되는지 특정해보는 것이 있습니다.

더 구체적으로 말하자면, 특정 지역의 크기를 증가 또는 감소시키는 factor 값을 측정해보는 것입니다.

예를 들어 열(3,0),(0,2)가 있을 때, 이 행렬은 i-hat(x축 단위 벡터)을 factor 3으로 확장시키고, j-hat(y축 단위 벡터)은 factor 2로 확장시키고 있습니다.
이는 11 정사각형에서 23 크기의 직사각형이 된걸 볼 수 있습니다.
처음엔 영역 크기가 1로 시작했는데, 나중에 영역 크기가 6이 된 것입니다.

따라서 이 선형변환을 factor 6으로 공간을 확장시킨다고 받아들일 수 있습니다.

이번에는 shear 변환을 나타내는 행렬을 예로 들어 설명해보겠습니다.
열(1,0),(1,1) 행렬은 i-hat은 변화시키기 않고, j-hat은 (1,1)로 이동시킵니다.
그러면 i-hat과 j-hat에 의해 결정된 단위 정사각형이, 기울여지는 변형 후에는 평행사변형이 됩니다.(그래도 평행사변형의 영역은 그대로 1입니다.)

따라서 이 선형변환의 전과 후 영역의 크기는 똑같습니다.

사실 하나의 정사각형 영역이 얼마나 변하는지 알게되면, 공간상 어떤 지역이 어떻게 변할지를 예측할 수 있습니다.

이러한 특별한 스케일링 factor는 선형변환에 의한 영역의 변화를 나타내는 factor로서 행렬식(determinant) 라고 부릅니다.

예를 들어, 한 변환의 행렬식 값이 3이라면, 특정 지역의 크기는 factor 3만큼 증가합니다.

만약 2차원 변환의 행렬식 값이 0이라면, 모든 공간이 찌부러뜨려져서 선이 될 수도 있거나, 어쩌면 한 점이 될 수도 있습니다. 그럼 당연히 어느 영역이든 크기는 0이 될 것 입니다.

그렇다면 영역을 스케일링할 때 음수값의 의미는 무엇일까요? 즉, 행렬식 값이 음수일 경우를 살펴보겠습니다.
이는 바로 방향(orientation)과 관계가 있습니다.

예를 들어, 공간의 방향을 뒤집는 변환(flipping)을 살펴보겠습니다.

또 다른 예를 들어, i-hat과 j-hat의 관계를 살펴보겠습니다.
벡터들의 시작 위치를 보면, i-hat이 j-hat의 오른쪽에 위치해있습니다. 하지만 변환 후에는(공간을 뒤집어보면) i-hat이 j-hat 왼쪽에 위치해있습니다.
즉 공간의 방향이 반전되어 있다는 걸 알 수 있습니다. 이럴때마다 행렬식의 값이 음수가 된다는 걸 알 수 있습니다. 하지만 행렬식의 절대값은 여전히 영역 스케일링에 관한 factor입니다.

행렬식의 값이 양수에서 0, 그리고 음수가 되는 과정을 살펴보겠습니다.

햏렬식의 값이 양수에서 0으로 갈 때, i-hat과 j-hat이 점점 가까워집니다. 그리고 비로소 0이 될 때 직선이 됩니다. 그리고 다시 음수가 될 때, 공간이 뒤집히는 것을 볼 수 있습니다.

여기까지가 2차원 행렬식에 대한 내용입니다. 그럼 3차원에서는 어떻게 될까요? 3*3 행렬식에서는 부피(volume)가 얼마나 스케일링 되는지 알려줍니다.

1x1x1 정육면체를 살펴보겠습니다. 이 정육면체의 모서리는 각각 i-hat, j-hat, k-hat으로 이루어져 있습니다.

이 정육면체는 변환 후 평행육면체(parallelepiped)가 됩니다. 즉, 이 행렬식은 평행육면체의 부피가 됩니다.

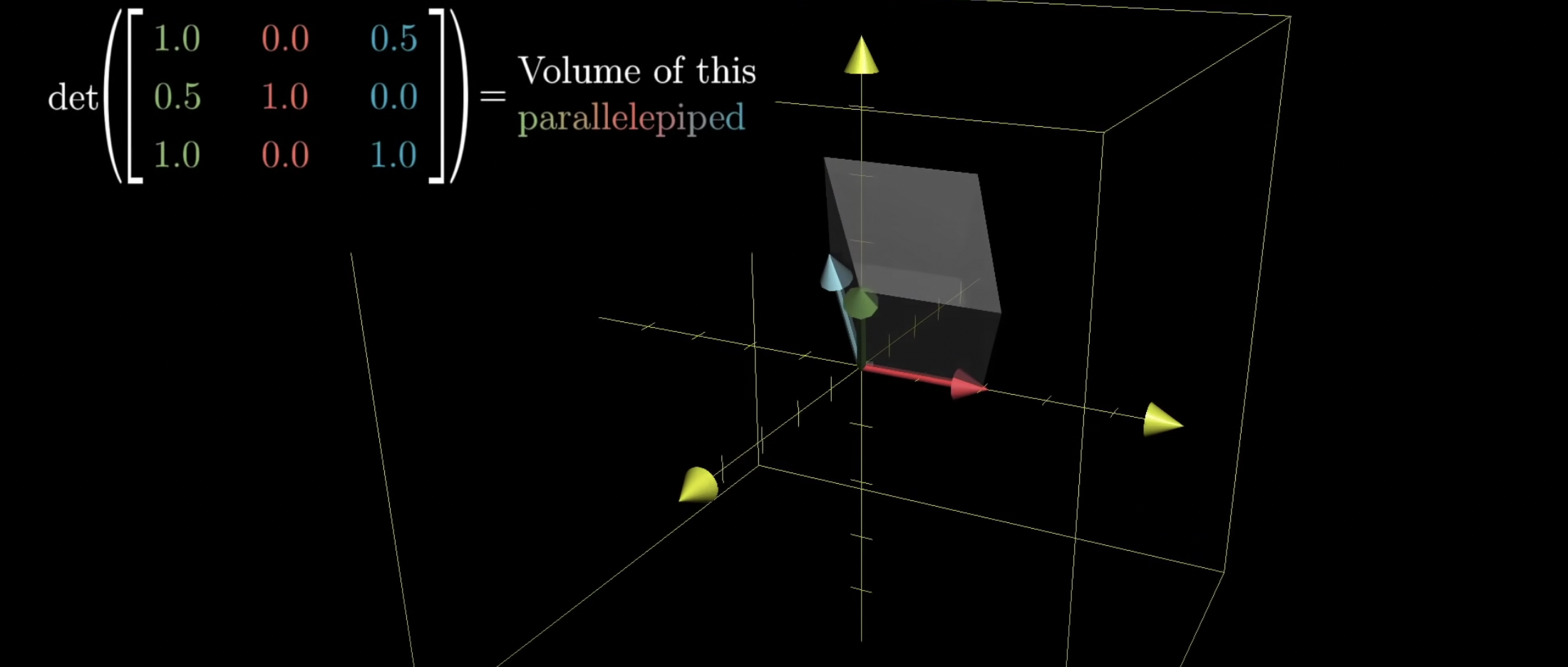
또 마찬가지로, 3차원에서 행렬식의 값이 0일 경우, 모든 공간을 찌부러뜨려서 부피를 0으로 만든다고 해석할 수 있습니다. 그래서 찌부러진 공간은 평면이나, 선, 가장 극단적인 경우에는 하나의 점이 될 수 있습니다.

그리고 저 행렬의 열들은 선형 종속이라고 표현할 수도 있습니다.

그렇다면 이제 실제로 행렬식을 계산하는 식을 살펴보겠습니다.
2*2 행렬에서 아래와 같이 이루어집니다.

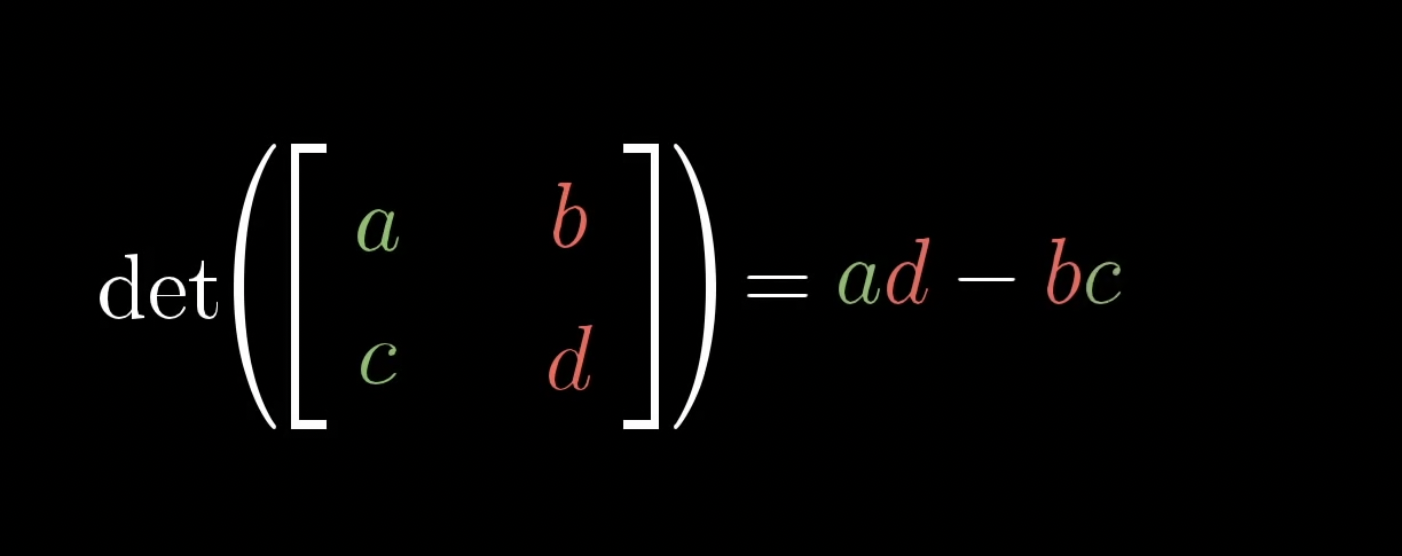
그렇다면 왜 이러한 식이 나왔는지 파헤쳐 보겠습니다.

먼저 위와 같은 식에서 b와 c를 0이라고 해보겠습니다.
그리고 a는 i-hat을 x축 방향으로 스케일링하는 요소로 보고, d의 경우에는 j-hat을 y축 방향으로 스케일링하는 요소로 보겠습니다.
그럼 다른 값(b, c)는 0이므로 행렬식 결과는 a*d가 됩니다.

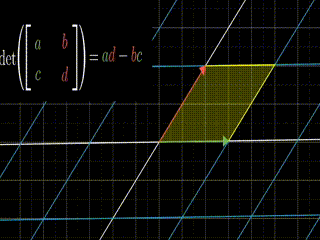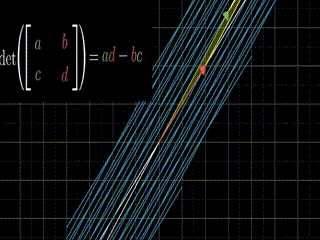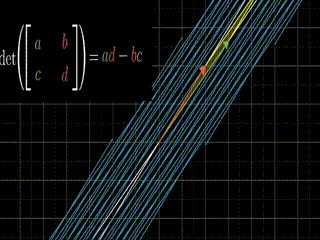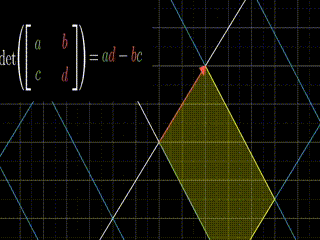
그리고 만약 b나 c 둘중 하나가 0이 아닐 경우에는, 평행사변형을 얻을 수 있습니다. 그럼 밑변 길이는 a, 높이는 d. 그럼 영역의 크기는 똑같이 a*d가 성립하게 됩니다.

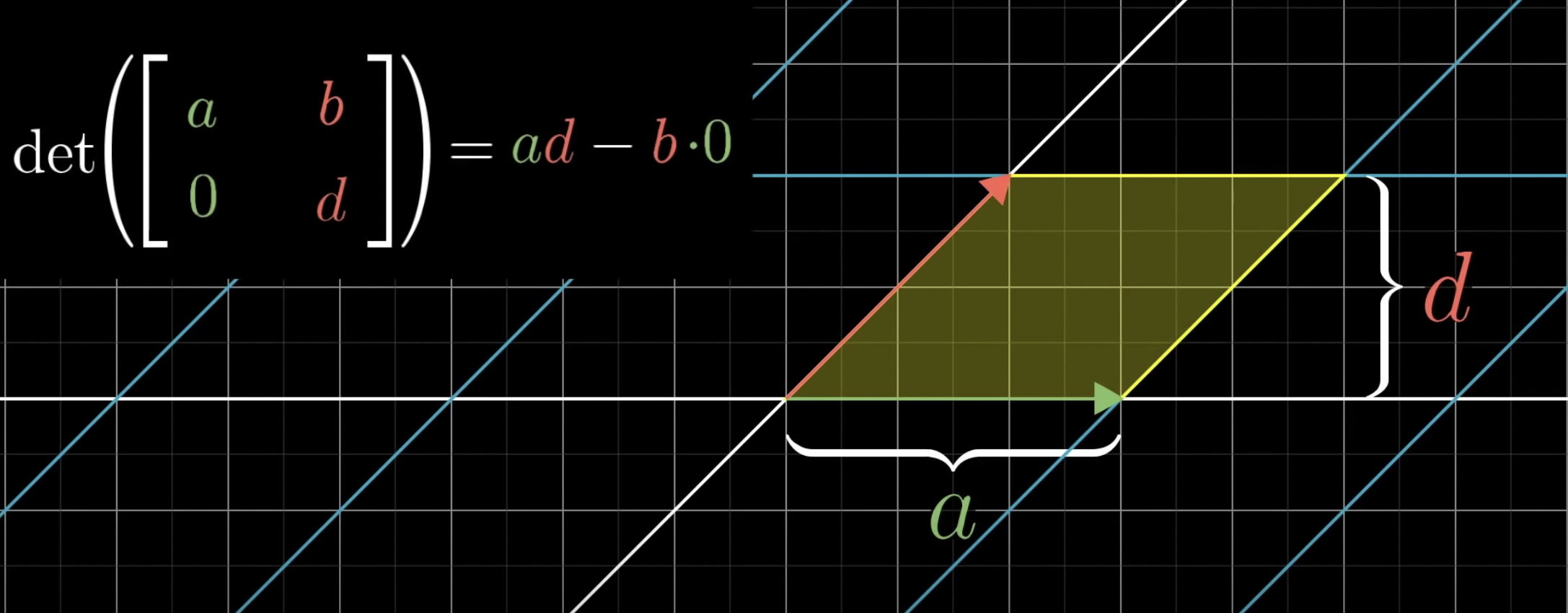
그리고 b와 c 둘다 0이 아닐 경우, b*c 값은 평행사변형이 얼마나 대각선방향으로 늘어나거나, 축소되는지 알려줍니다.

3차원에서 행렬식의 계산 과정은 아래와 같습니다.

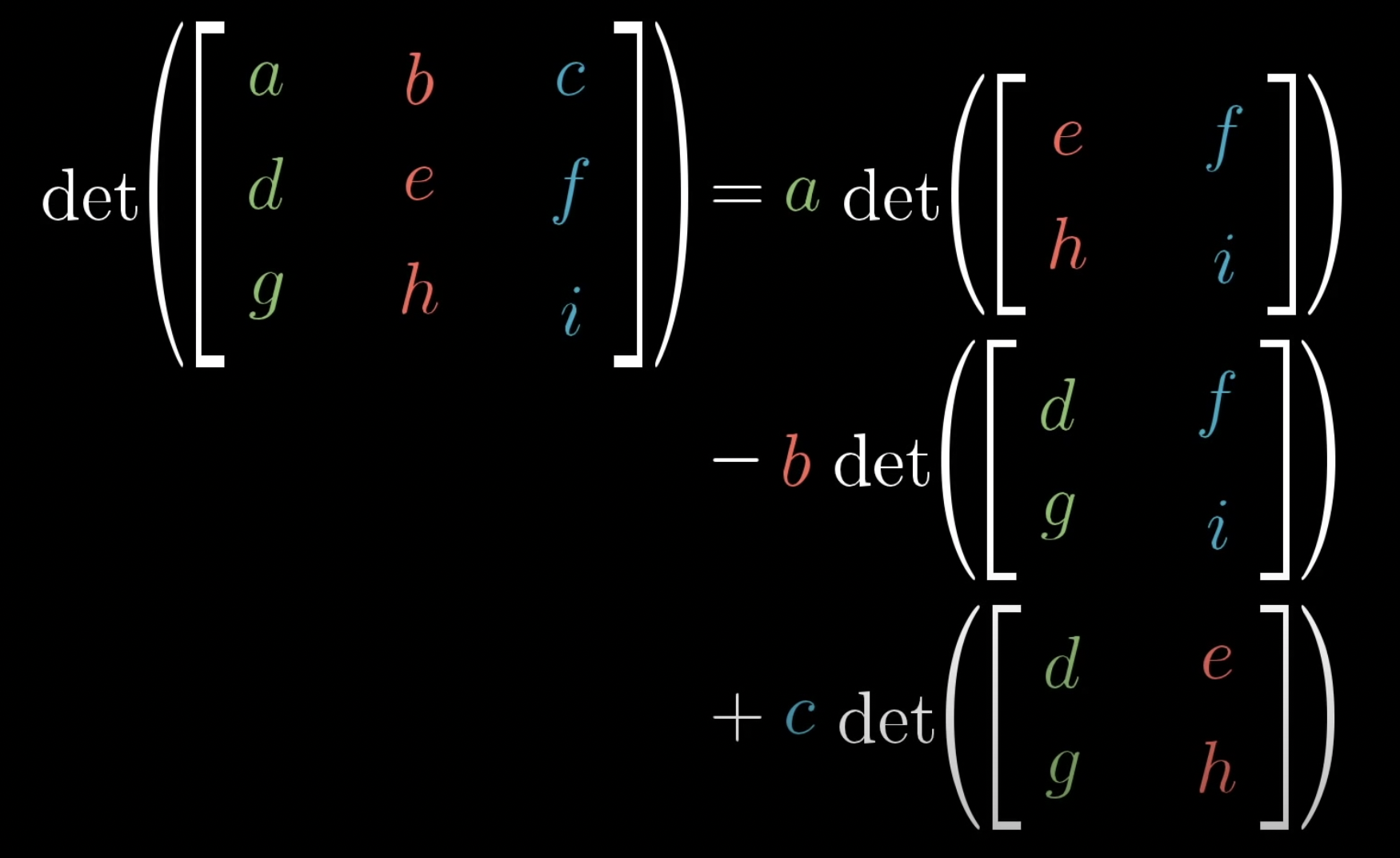
Summary

이번 시간에는 행렬식에 대해 살펴보았습니다.

다음 장에서는 지금까지 배운 선형 변환의 개념을 다른 것과 엮어볼 것입니다. 선형 방정식을(linear system of Equations) 배우고, 역행렬(Inverse Matrices), column space, null space에 대해 배워보겠습니다.

Reference

1. https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab