해당 글은 3Blue1Brown 채널의 Essence of linear algebra를 정리한 스터디 노트입니다.

Chapter 5. Essence of linear algebra

이번에는 3차원 벡터를 입력받아 3차원 벡터를 출력해보겠습니다.

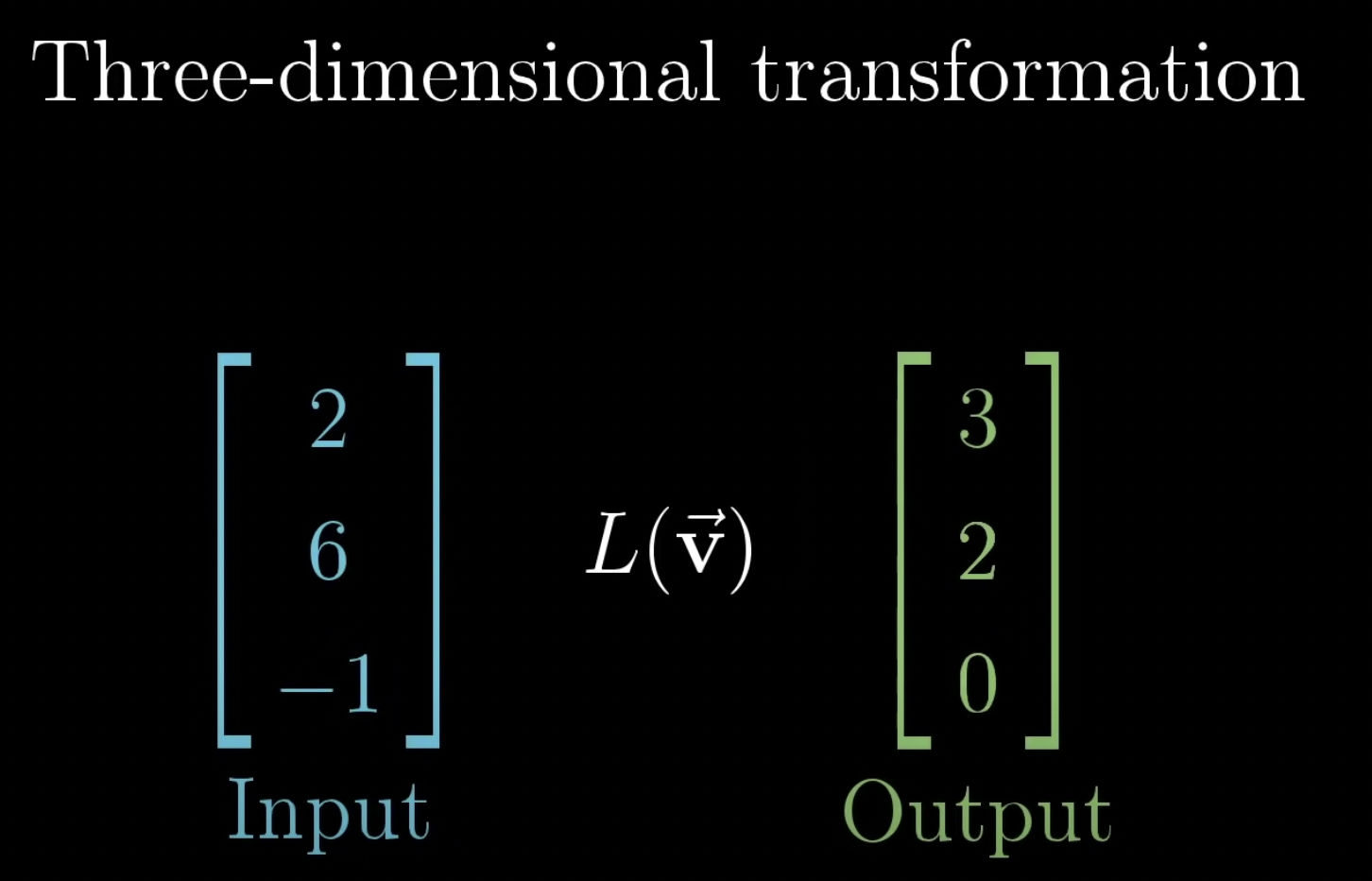
이를 기하학적인 측면에서 각 기저벡터로 표현해보면, 다음과 같습니다.
qQV4OR

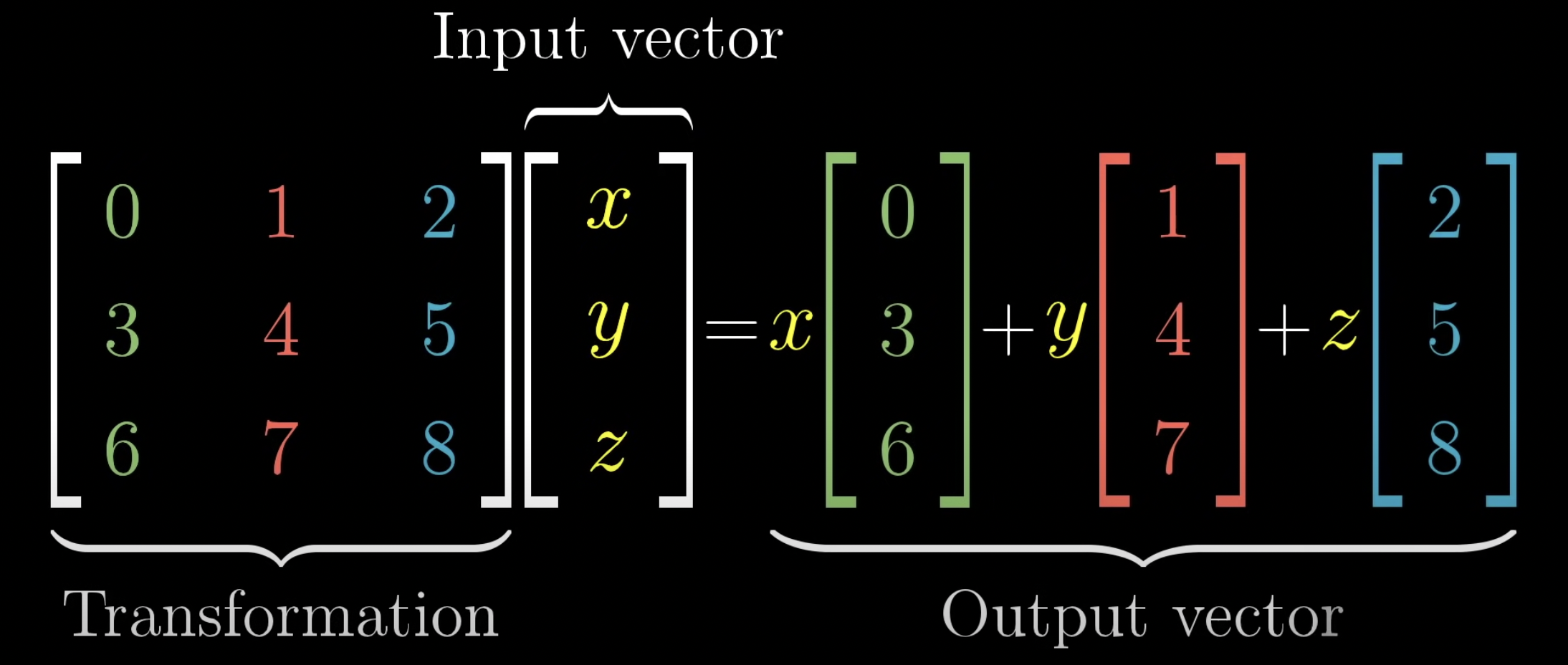
3가지 좌표 값의 집합이 행렬의 열을 구성하게 됩니다. 그리고 저 행렬이 어떠한 변환을 나타내게 됩니다.

어떤 벡터 [x,y,z]가 변환 후 어디가 되는지는, 각 좌표값을 스케일링 벡터로 보면 알 수 있습니다. 각 기저벡터들은 그 팩터로 스케일링해서 합치면 원하는 결과벡터를 얻게 됩니다.
28gBjj

그래서 벡터의 변환 결과를 알려면, 벡터의 좌표값을 행렬의 대응되는 열과 곱한다음 그 결과를 합하면 됩니다.

두 개의 행렬을 곱할 때마다 항상 오른쪽 행렬로 먼저 변환처리가 되고, 그리고나서 왼쪽 행렬 적용됨.

Summary

이번 시간에는 3차원의 행렬 곱에 대해 살펴보았습니다.

다음 장에서는 행렬의 결정식(determinant)에 대해 살펴보겠습니다.