[Linear Algebra] Matrix multiplication as composition
해당 글은 3Blue1Brown 채널의 Essence of linear algebra를 정리한 스터디 노트입니다.
Chapter 4. Essence of linear algebra
선형변환을 하고 나서 거기에 다시 선형변환을 하는 것도 가능합니다.
예를 들어 시계방향으로 90도 회전(rotation)을 시키고, 그리고 나서 옆으로 밀면(shear) 어떻게 되는지 아래를 통해 알 수 있습니다.
전체효과는 이것들 또한 또 하나의 선형변환입니다. 그리고 이를 두 개의 선형 변환의 합성(composition)이라고 일컫습니다.

합성된 선형변환도 행렬로 표현이 가능합니다. 이전과 마찬가지로 i-hat, j-hat을 이용하면 됩니다.
여기서 i-hat의 최종 도착지는 (1,1)이 됩니다. 그럼 이것을 행렬의 첫 번째 열로 적으면 됩니다. 그리고 j-hat의 최종 도착지는 (-1,0)이 되며, 이것을 행렬의 두 번째 열로 적으면 완성됩니다.
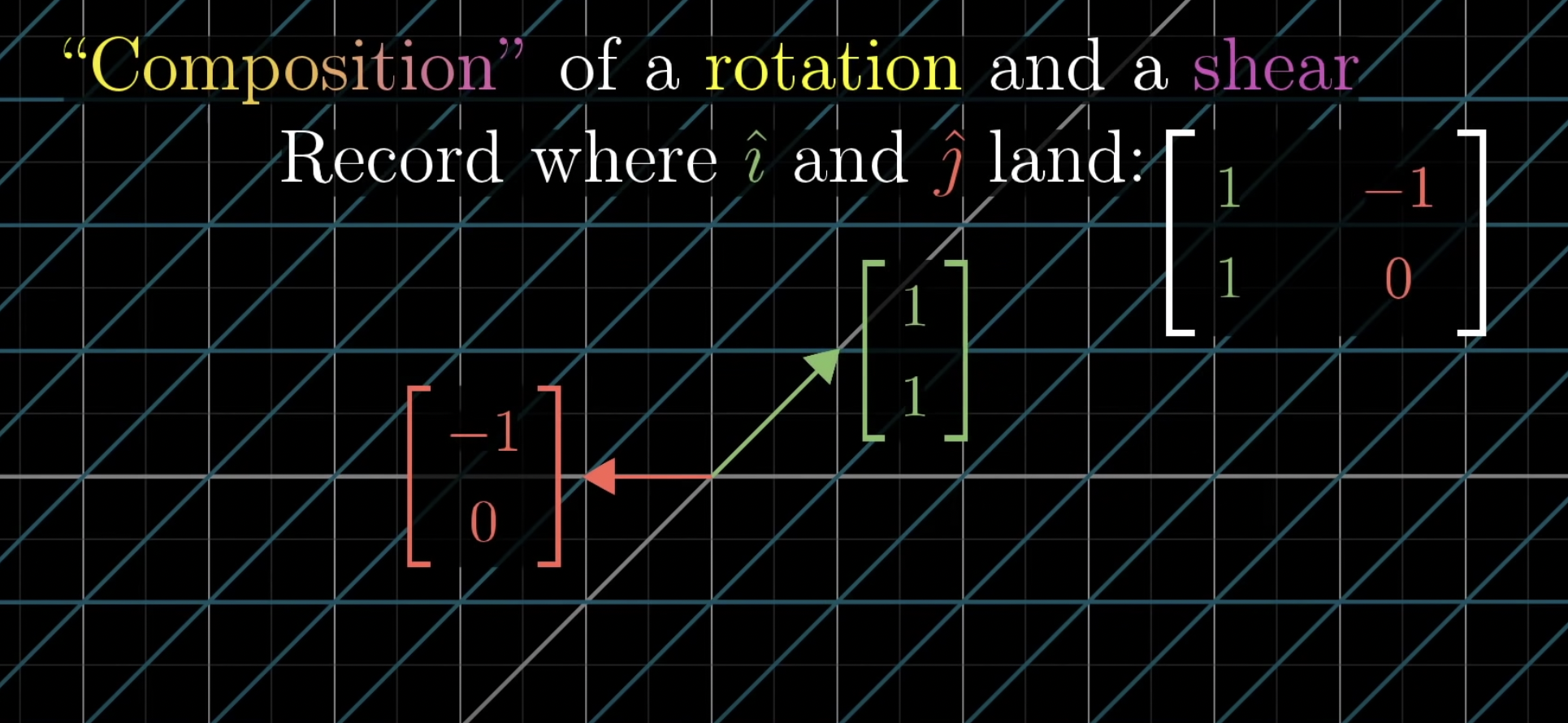
그럼 이 행렬이 "Composition" of a rotation and shear의 결과물이 됩니다.
이 과정을 수치적으로 표현하면 아래와 같습니다.
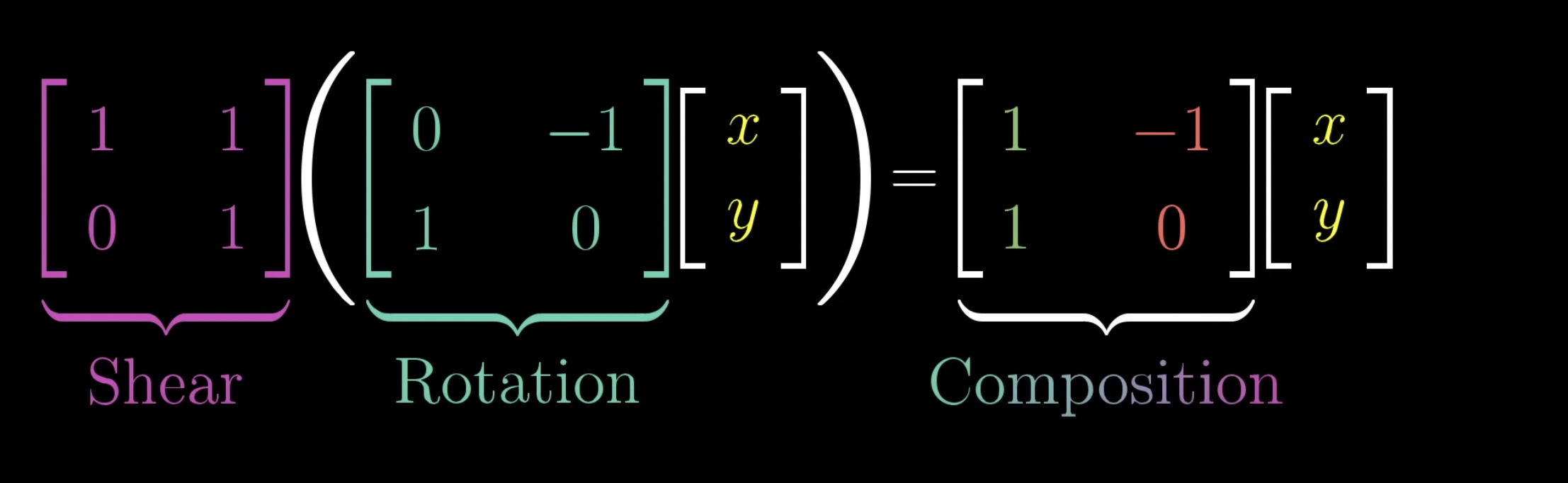
위 표현을, 두 행렬의 곱(product) 으로 바꿔 말할 수 있습니다. 그리고 두 행렬의 곱은 기하학적으로 한 변환을 적용하고 나서, 다른 변환을 적용한 것과 같습니다.
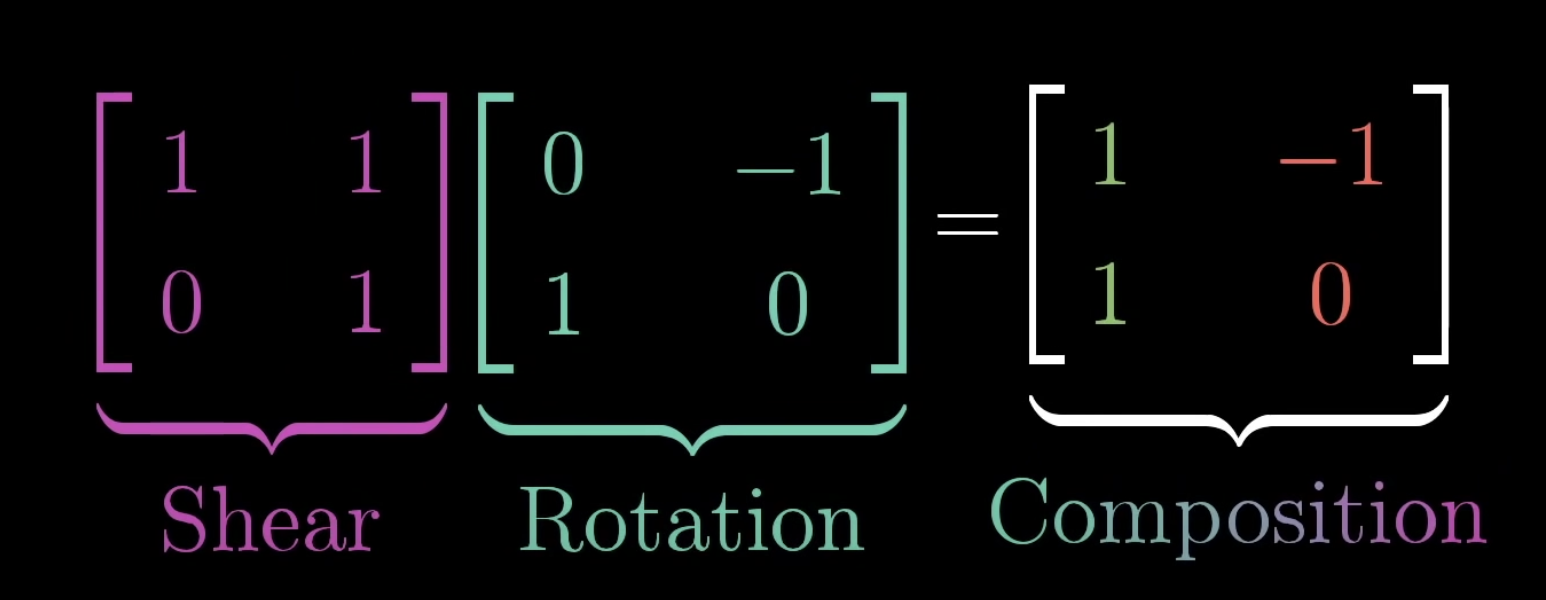
이번에는 두 행렬의 곱 연산 과정을 기하학적으로 살펴보겠습니다.
먼저 M1의 행렬의 변환은 다음과 같습니다. (이는 i-hat, j-hat 기저벡터에서 M1의 행렬 변환을 적용시킨 것입니다.)

다음은 M2의 행렬 변환입니다.

최종 matrix product 결과는 다음과 같습니다.

행렬 곱 성질(properties of matrix product)
앞서 살펴본 예제로 M1과 M2 행렬이 있습니다. 이 두 행렬을 곱할 때 과연 곱하는 순서가 상관이 있을까요?
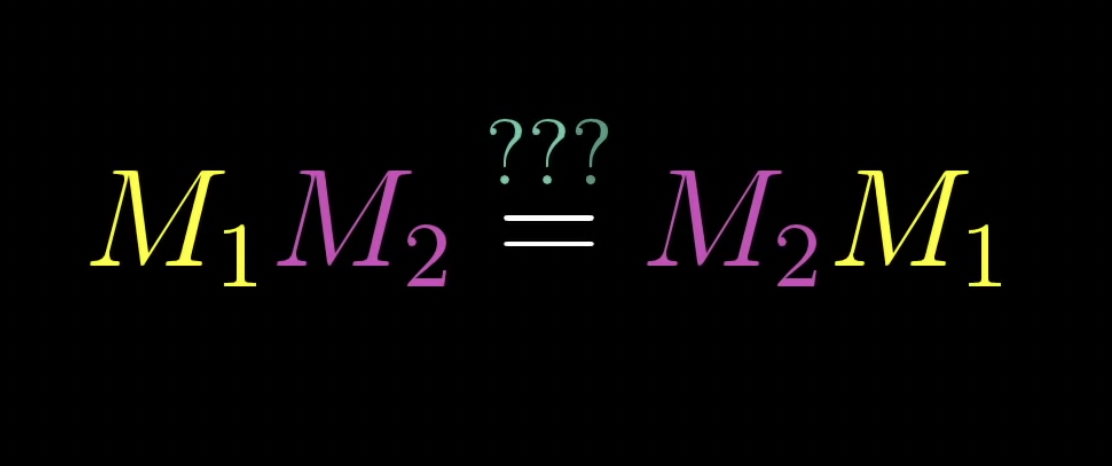
앞서 활용했던 예제를 통해 검증해보겠습니다.
shear변환(i-hat은 고정이고 j-hat만 오른쪽으로 밀어지는)과 rotation 변환을 이용해보겠습니다.
- shear 변환 -> rotation 변환(M1->M2) 결과:

- rotation 변환 -> shear 변환(M2->M1) 결과:

이 둘의 결과 벡터는 서로 다른 좌표값을 가지고 있습니다. 따라서 곱하는 순서에 따라 결과가 달라지기 때문에 순서는 중요하다고 할 수 있습니다.
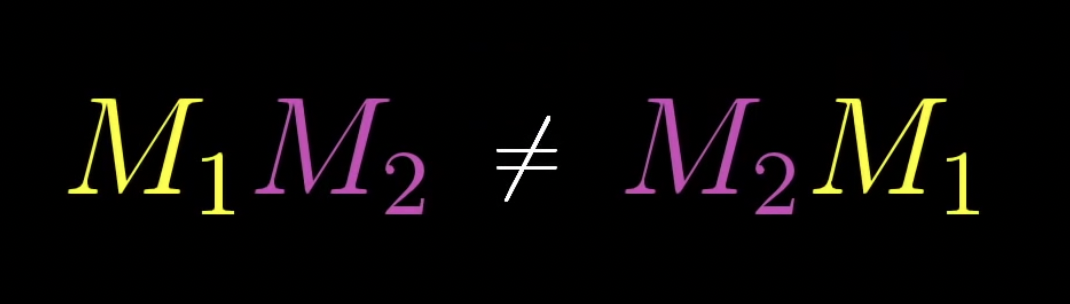
다음은 행렬의 결합법칙(Associativity) 성립에 대해 검증해보겠습니다.
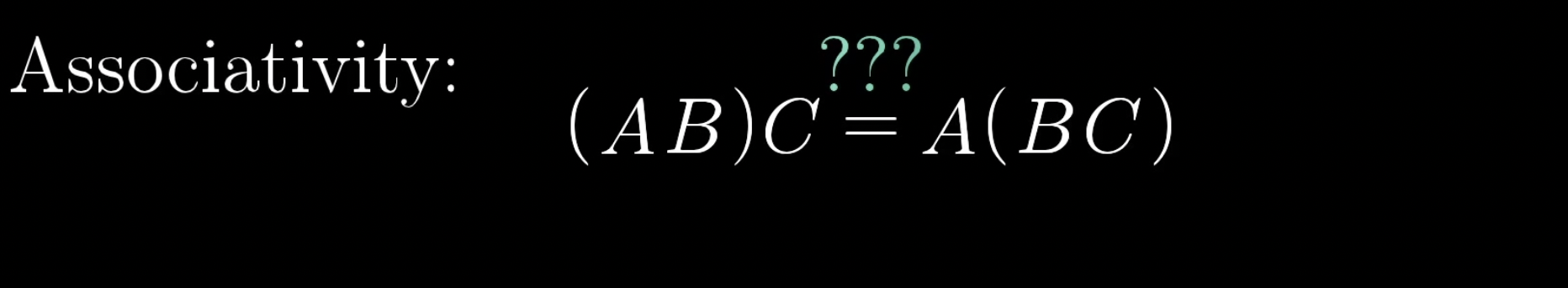
기하학적인 측면에서 그냥 동일한 세 변환을 같은 순서대로 적용해보면 결합법칙이 성립한다는 것을 매우 쉽게 알 수 있습니다.

(AB)C의 연산 과정:

A(BC)의 연산 과정:

Summary
이번 시간에는 행렬 곱에 대해 살펴보았습니다.
다음 장에서는 3차원에서 두 행렬의 곱셈에 대해 살펴보겠습니다.
Reference
- https://www.youtube.com/playlist?list=PLZHQObOWTQDPD3MizzM2xVFitgF8hE_ab
