저자 Dasgupta의 Algorithms을 해석하면서 정리한 글입니다.

2.1 Multiplication

Given two n-bit positive integers x and y, calculate their product

문제 자체는 두 정수를 곱하라는 내용입니다. 평소 우리는 대부분 정수 곱셈을 $O(1)$만에 합니다.
하지만 굉장히 큰 두 정수가 주어졌을 때, divied & conquer을 사용하여 곱셈을 할 수 있습니다.

우선 자연스럽게 n-bit 짜리 X와 Y를 2개로 쪼개보겠습니다.

$x =x_1 \cdot 2^{\lfloor{n/2}\rfloor}+x_0$

$y = y_1 \cdot 2^{\lfloor{n/2}\rfloor}+y_0$

그림으로 표현하면 아래와 같습니다.

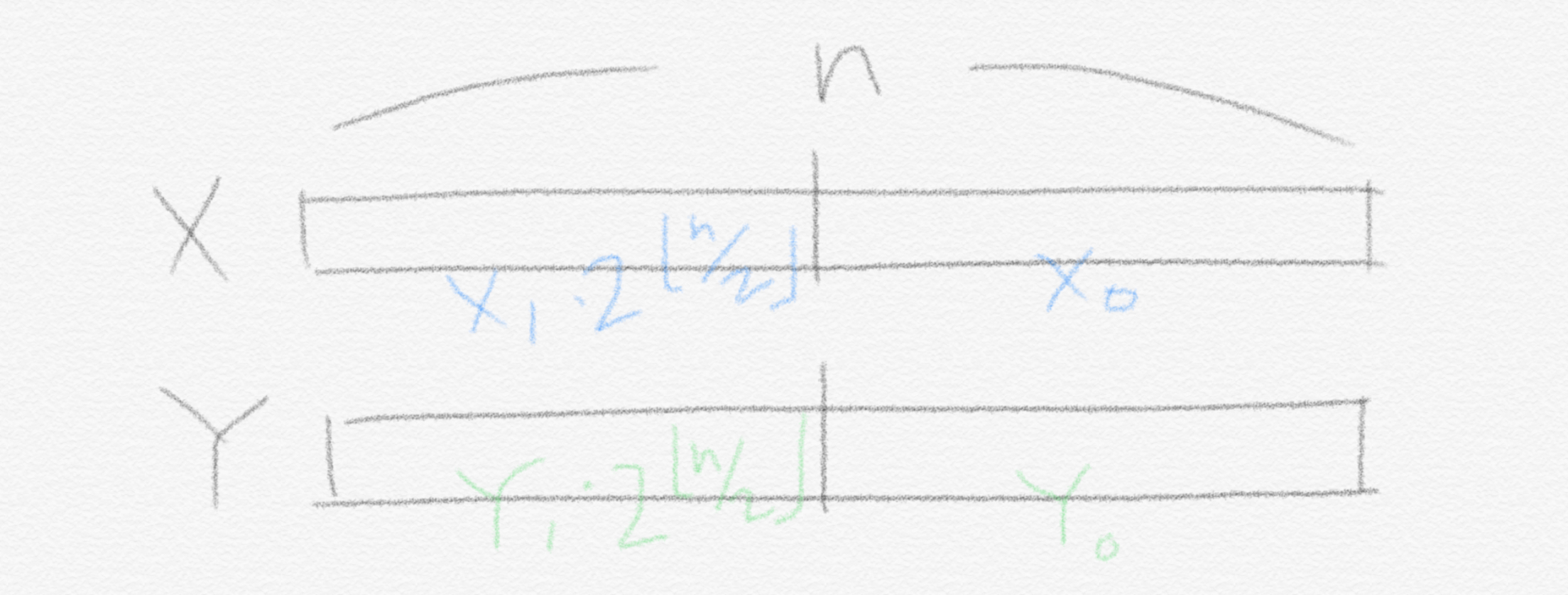
그리고 x와 y를 곱하면 이런 식이 완성됩니다.

$xy = x_1y_1\cdot 2^{2\lfloor{n/2}\rfloor} + (x_0y_1+x_1y_0)2^{\lfloor{n/2}\rfloor} +x_0y_0$

우리는 x를 $x_1$, $x_0$으로 y를 $y_1$, $y_0$으로 나누었습니다. 이를 각각 하나의 subproblem으로 볼 수 있습니다. 이 모두를 알고리즘으로 나타내보겠습니다.

1차 알고리즘

function Multiply(x,y)
    if n<=3:
        do the elementary math
    p_1 = Multiply(x_1, y_1)
    p_2 = Multiply(x_0, y_1)
    p_3 = Multiply(x_1, y_0)
    p_4 = Multiply(x_0, y_0)

    sol = p_1*2^{2*(n/2)}+(p_2+p_3)*2^{n/2}+p_4

    return sol

각각 쪼갠 subproblem들로 구해서 답을 내줍니다.

이제 위 알고리즘의 시간 복잡도를 계산해보겠습니다. 위 알고리즘의 시간 복잡도는 $O(n^2)$입니다.

Divide & Conquer 방식의 알고리즘은 시간복잡도 계산을 매우 편리하게 theorem이 존재합니다. 바로 Master theorem이라고 불리는 이론입니다.

Master theorem
단순히 아래 식 parameter인 a, b, f(n)의 시간복잡도만 넣어주면 Divide & conquer의 시간복잡도가 계산이 되는 편리한 정리입니다.

• $a$: divide & conquer에서 몇 개의 subproblem으로 나누는지, 한 레벨에서 재귀가 몇 번 불리는지 (subproblem의 개수)
• $b$: subproblem에 들어가는 input size가 기본 input 대비 줄어드는 비율의 역수
  • ex) subproblem / problem 개수
• $f(n)$: subproblem들을 combine하는 merging step에 드는 시간복잡도
  • ex) $a = 2$, $b = 2, f(n) = O(n)$일 때는 $log_22$ = 1인데, $\epsilon$은 0이 아닌 양수이므로 $n^1$을 만들 수 없습니다. 따라서 2번의 경우에서 $k = 0$인 경우라고 할 수 있습니다.

이를 지금 문제에 적용해보겠습니다. 위에서 하나의 Multiply(x,y)가 4개의 Multiply()를 호출합니다. 그리고 각 subproblem은 원래의 problem보다 크기가 1/2 줄어든 input을 받게 됩니다.
그러므로 $a = 4, b = 2$ 입니다. 마지막으로 merging step에서는 2를 곱한다는 것은 bit를 앞쪽으로 한칸 씩 미는 것 입니다. 그러므로 liner time $O(n)$에 가능합니다.

이에 따라 1번 case를 적용시켜 $T(n) = \Theta(n^{log_24})$가 되어 $\Theta(n^2)$의 시간복잡도가 나옵니다.

2차 알고리즘

위 알고리즘보다 더 좋은 알고리즘을 만들 수 있습니다. 이유는 아래와 같습니다.

$x_1y_0+x_0y_1 = (x_1 + x_0)(y_1 + y_0) - x_1y_1 - x_0y_0$

이렇기 때문에 굳이 p_2 = Multiply(x_0, y_1), p_3 = Multiply(x_1, y_0)를 추가적으로 부를 필요가 없습니다. 이미 갖고 있는 정보들을 이용해 조합을 하면 되기 때문입니다.

function Multiply(x,y)
    if n<=3:
        do the elementary math
    p_1 = Multiply(x_1+x_0, y_1+y_0)
    p_2 = Multiply(x_1, y_1)
    p_3 = Multiply(x_0, y_0)

    sol = p_2*2^{2*(n/2)}+(p_1-p_2-p_3)*2^{n/2}+p_3

    return sol

이렇게 Multiply() 호출 횟수가 줄었습니다. 그래서 다시 시간복잡도를 계산하기 위해 master theorem을 이용하면, $a = 3, b = 2$가 되어 총 시간복잡도는 $T(n)=\Theta (n^{log_2 4})$입니다.

Conclusion

Devide & conquer에서는 배타적인 subproblem들로 문제를 나누어 각각에서 해답을 구하고 그것들을 이용해 최종 답을 이끌어내는데 이용합니다.

subproblem들이 나뉘어지는 경계선에 optimal solution이 걸쳐있는 경우가 존재할 때 merging(combining) step에서 이를 고려하여야 합니다.
divide & conquer에서는 이런 사실을 간과하기 쉬우므로 늘 조심해야 합니다.

Reference

1. Algorithms - Dasgupta
2. https://hyunw.kim/blog/2018/09/18/Algorithm_Analysis02_Divide&Conquer.html