[DeepLearning] CH03. 신경망 시작하기(4)

in Deep Learning on Deeplearning


케라스 창시자에게 배우는 딥러닝을 기반으로 공부한 내용을 정리합니다.

3.6 주택 가격 예측: 회귀 문제

이번 장에서는 연속적인 값을 예측하는 회귀(regression)문제를 다뤄보겠습니다.

logistic regression은 분류 알고리즘이므로 혼동하면 안됩니다.

3.6.1 보스턴 주택 가격 데이터셋

1970년 중반 보스턴 외곽 지역의 범죄율, 지방세율 등의 데이터가 주어졌을 때 주택 가격의 중간 값을 예측해 보겠습니다.

데이터 포인트가 506개로 비교적 개수가 적고 404개는 훈련 샘플로, 102개는 테스트 샘플로 나뉘어 있습니다.

입력 데이터에 있는 각 feature(Ex. 범죄율)은 스케일이 서로 다릅니다. 어떤 값은 0과 1 사이의 비율을 나타내고, 어떤 것은 1과 100 사이의 값을 가질 수도 있습니다.

# code 3-24 보스턴 주택 데이터셋 로드하기
from keras.datasets import boston_housing

(train_data, train_targets), (test_data, test_targets) = boston_housing.load_data()

>>> train_data.shape
(404, 13)

>>> test_data.shape
(102, 13)

>>> train_targets
[15.2, 42.3, 50., ..., 19.4, 19.4, 29.1]

이 13개의 수치 특성들은 1인당 범죄울, 주택당 평균 방의 개수, 고속도로 접근성 등이 있습니다. 타깃은 주택의 중간 가격으로 천 달러 단위입니다.

3.6.2 데이터 준비

만약 서로 다른 스케일을 가진 값을 신경망에 주입하면 문제가 발생할 수 있습니다. 기본적으로 네트워크가 다양한 데이터에 자동으로 맞추려고 할 수 있지만 학습을 어렵게 만듭니다.

특성의 스케일이 다르면 전역 최소 점을 찾아가는 경사 하강법의 경로가 스케일이 큰 특성에 영향을 많이 받습니다.

따라서 특성별로 정규화를 거쳐야 합니다.

입력데이터에 있는 각 특성에 대해서 특성의 평균을 빼고 표준 편차로 나눕니다. 특성의 중앙이 0 근처에 맞추어지고 표준 편차가 1이 됩니다.

#  code 3-25 data nomalizaion
mean = train_data.mean(axis = 0)
train_data -= mean
std = train_data.std(axis = 0)
train_data /= std

test_data -= mean
test_data /= std

정규화 과정에서 절대로 테스트 데이터에서 계산한 어떤 값도 사용해서는 안됩니다.

3.6.3 모델 구성

일반적으로 훈련 데이터의 개수가 적을수록 overfitting이 더 쉽게 일어나므로 작은 모델을 사용하는 것이 overfitting을 피하는 방법입니다.

# code 3-28 모델 정의하기
from keras import models
from keras import layers

def build_model():
    model = models.Sequential()
    model.add(layers.Dense(64, activation='relu'), input_shape=(train_data.shape[1], ))
    model.add(layers.Dense(64, activation='relu'))
    model.add(layers.Dense(1))
    model.compile(optimizer='rmsprop', loss='mse', metrics=['mae'])
    return model

이 네트워크의 마지막 층은 활성화 함수가 없습니다. 이것이 전형적인 스칼라 회귀(하나의 연속적인 값을 예측하는 회귀)를 위한 구성입니다.

이 모델은 mse 손실 함수를 사용하여 컴파일합니다. 이 함수는 평균 제곱 오차(mean squared error)으로 예측과 타깃 사이 거리의 제곱입니다. 회귀 문제에서 널리 사용되는 손실 함수 입니다.

훈련하는 동안 평균 절대 오차(Mean Absolute Error, MAE)를 측정합니다. 이는 예측과 타깃 사이 거리의 절댓값입니다.

3.6.4 K-겹 검증을 사용한 훈련 검증

데이터 포인트가 많지 않기 때문에 검증 데이터 세트도 매우 작아집니다(약 100개 samples). 검증 세트의 분할에 대한 검증 점수의 분산이 높으면 신뢰 있는 모델 평가를 할 수 없습니다.

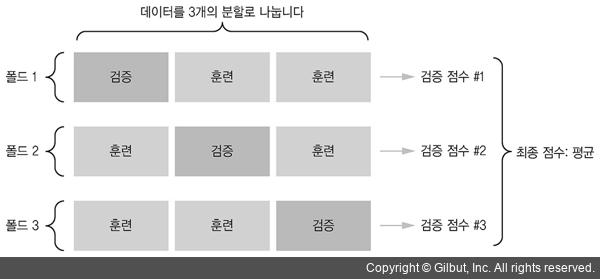
따라서 K-겹 교차 검증(K-fold cross-validation)을 사용해야 합니다. 데이터를 K개의 분할(즉 폴드(fold))로 나누고(일반적으로 K=4 또는 5), K개의 모델을 각각 만들어 K-1개의 분할에서 훈련하고 나머지 분할에서 평가하는 방법입니다. 모델의 검증 점수는 K개의 검증 점수 평균이 됩니다.

img

# code 3-27 K-겹 검증하기
import numpy as np

k = 4
num_val_samples = len(train_data) // k
num_epochs = 100
all_scores = []

for i in range(k):
    print('처리중인 폴드 #', i)
    val_data = train_data[i * num_val_samples: (i+1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]

    partial_train_data = np.concatenate( 
        [train_data[:i * num_val_samples],
        train_data[(i + 1) * num_val_samples:]],
        axis = 0)
    
    partial_train_target = np.concatenate(
        [train_targets[:i * num_val_samples],
        train_targets[(i + 1) * num_val_samples:]],
        axis = 0)
    
    model = build_model()
    model.fit(partial_train_data, partial_train_target,
                epochs=num_epochs, batch_size = 1, verbose=0) # verbose = 0이므로 훈련과정 출력x
    val_mse, val_mae = model.evaluate(val_data, val_targets, verbose = 0)
    all_scores.append(val_mae)

concatenate 함수는 배열 결합 함수입니다.

실행 결과

>>> all_scores
[2.0956787838, 2.2205937970, 2.859968412, 2.4053570403]

>>> np.mean(all_scores)
2.395399508

검증 세트가 다르므로 확실히 검증 점수가 2.1에서 2.9까지 변화가 큽니다. 평균값(2.4)이 각각의 점수보다 훨씬 신뢰할 만합니다.

이 예에서는 평균적으로 2,400달러 정도 차이가 납니다.

# code 3-28 각 폴드에서 검증 점수를 로그에 저장하기
num_epochs = 500
all_mae_histories = []
for i in range(k):
    print('처리중인 폴드 #', i)
    val_data = train_data[i * num_val_samples: (i + 1) * num_val_samples]
    val_targets = train_targets[i * num_val_samples: (i + 1) * num_val_samples]
    partial_train_data = np.concatenate( 
        [train_data[:i * num_val_samples],
         train_data[(i + 1) * num_val_samples:]],
        axis=0)
    partial_train_targets = np.concatenate(
        [train_targets[:i * num_val_samples],
         train_targets[(i + 1) * num_val_samples:]],
        axis=0)

model = build_model() 
history = model.fit(partial_train_data, partial_train_targets,
                    validation_data=(val_data, val_targets),
                    epochs=num_epochs, batch_size=1, verbose=0)
mae_history = history.history['val_mean_absolute_error']
all_mae_histories.append(mae_history)

그 다음 모든 폴드에 대해 epochs의 MAE 점수 평균을 계산합니다.

# code 3-29 K-겹 검증 점수 평균을 기록하기
average_mae_history = [
    np.mean([x[i] for x in all_mae_histories]) for i in range(num_epochs)]

이를 그래프로 표현해보겠습니다.

# code 3-30 검증 점수 그래프
import matplotlib.pyplot as plt

plt.plot(range(1, len(average_mae_history) + 1), average_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

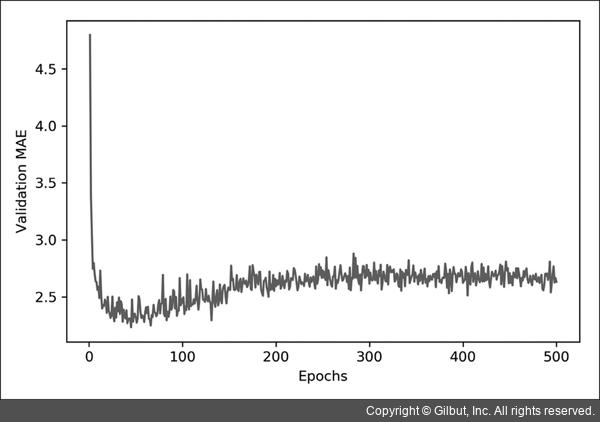img 에포크별 검증 MAE

위 그래프는 범위가 크고 변동이 심하여 보기가 좀 어렵습니다. 따라서

  • 곡선의 다른 부분과 스케일이 많이 다른 첫 10개의 데이터 포인트를 제외시킵니다.
  • 부드러운 곡선을 얻기 위해 각 포인트를 이전 포인트의 지수 이동 평균(exponential moving average)으로 대체합니다.
# code 3-31 처음 10개의 데이터 포인트를 제외한 검증 점수 그리기
def smooth_curve(points, factor=0.9):
    smoothed_points = []
    for point in points:
        if smoothed_points:
            previous = smoothed_points[-1]
            smoothed_points.append(previous * factor + point * (1 - factor))
        else:
            smoothed_points.append(point)
    return smoothed_points

smooth_mae_history = smooth_curve(average_mae_history[10:])

plt.plot(range(1, len(smooth_mae_history) + 1), smooth_mae_history)
plt.xlabel('Epochs')
plt.ylabel('Validation MAE')
plt.show()

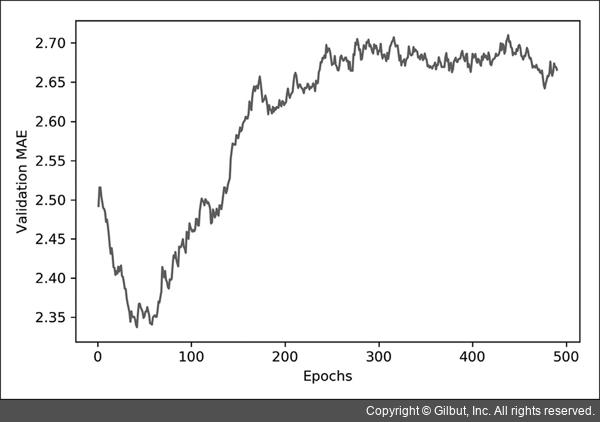img 처음 10개의 데이터 포인트를 제외한 에포크별 검증 MAE

그래프를 보면 검증 MAE가 80번째 에포크 이후에 줄어드는 것이 멈추었습니다. 이 지점 이후로는 overfitting이 발생하는 것을 알 수 있습니다.

# code 3-32 최종 모델 훈련하기
model = build_model() # 새롭게 컴파일된 모델을 얻습니다.
model.fit(train_data, train_targets,
        epochs=80, batch_size=16, verbose=0)
test_mse_score, test_mae_score = model.evaluate(test_data, test_targets)

# 최종 결과
>>> test_mae_score
2.675027286

3.6.5 정리

  • 회귀는 평균 제곱 오차(MSE) 손실 함수를 주로 사용합니다.
  • 정확도 개념은 회귀에 적용되지 않습니다. 일반적인 지표로 평균 절대 오차(MAE)입니다.
  • 입력 데이터의 특성이 서로 다른 범위를 가지면 전처리 단계에서 각 특성을 개별적으로 스케일 조정해야 합니다.
  • 가용한 데이터가 적다면 K-겹 검증을 사용하는 것이 신뢰할 수 있는 모델 평가 방법입니다.
  • 가용한 훈련 데이터가 적다면 overfitting을 피하기 위해 hidden layers의 수를 줄인 모델이 좋습니다(일반적으로 1개 또는 2개).

3.7 요약

마지막으로 3장에 배운 것들을 정리해보겠습니다.

  • 보통 원본 데이터를 신경망에 주입하기 전에 전처리 과정을 거쳐야 합니다.
  • 데이터에 범위가 다른 특성이 있다면 전처리 단계에서 각 특성을 독립적으로 스케일 조정해야 합니다.
  • 훈련이 진행됨에 따라 신경망의 과대적합이 시작되면 새로운 데이터에 대해 나쁜 결과를 얻게 됩니다.
  • 훈련 데이터가 많지 않으면 overfitting을 피하기 위해 1개 또는 2개의 은닉 층을 가진 신경망을 사용합니다.
  • 데이터가 많은 범주로 나뉘어 있을 때 중간층이 너무 작으면 정보의 병목이 생길 수 있습니다.
  • 적은 데이터를 사용할 때는 K-겹 검증이 신뢰할 수 있는 모델 평가를 도와줍니다.



Reference

  1. 케라스 창시자에게 배우는 딥러닝
  2. https://data-make.tistory.com/132



© 2020. by GeonKimdcu

Powered by aiden