케라스 창시자에게 배우는 딥러닝을 기반으로 공부한 내용을 정리합니다.

2.4 신경망의 엔진: 그래디언트 기반 최적화

output = relu(dot(W, input) + b)
이 식에서 텐서 W와 b는 층의 속성처럼 볼 수 있습니다. 가중치(weight) 또는 훈련되는 파라미터(trainable parameter)라고 부릅니다(각각 커널(kernel)과 편향(bias)이라고 부르기도 합니다).
이런 가중치에는 훈련 데이터를 신경망에 노출시켜서 학습된 정보가 담겨져 있습니다.

초기에는 가중치 행렬이 작은 난수로 채워져 있습니다(무작위 초기화(random initialization)단계라고 부릅니다). 물론 W와 b가 난수일 때 relu(dot(W, input) + b)가 유용한 어떤 표현을 만들 것이라고 기대할 수는 없습니다. 즉 의미 없는 표현이 만들어집니다. 하지만 이는 시작 단계일 뿐입니다. 피드백 신호에 기초하여 가중치가 점진적으로 조정될 것입니다. 이런 점진적인 조정 또는 훈련(training)이 머신러닝 학습의 핵심입니다.

훈련은 다음과 같은 훈련 반복 루프 안에서 일어납니다. 필요한 만큼 반복 루프 안에서 이런 단계가 반복됩니다.

1. 훈련 샘플 x와 이에 상응하는 타깃 y의 배치를 추출합니다.
2. x를 사용하여 네트워크를 실행하고(정방향 패스(forward pass)단계), 예측 y_pred를 구합니다.
3. y_pred - y = 오차를 측정하여 이 배치에 대한 네트워크의 손실을 계산합니다.
4. 배치에 대한 손실이 조금 감소되도록 네트워크의 모든 가중치를 업데이트합니다.(loss가 0으로 수렴할 때 까지)

결국 훈련 데이터에서 네트워크의 손실, 즉 예측 y_pred와 타깃 y의 오차가 매우 작아질 것입니다.

개별적인 가중치 값이 있을 때 값이 증가해야 할지 감소해야 할지, 또 얼만큼 업데이트해야 할지 어떻게 알 수 있을까요?

가중치의 업데이트한 값을 토대로 손실에 기여한 바를 파악하는 방식은 비효율적입니다.
신경망에 사용된 모든 연산이 미분 가능(differentiable)하다는 장점을 사용하여 네트워크의 가중치에 대한 손실의 그래디언트(gradient)를 계산하는 것이 훨씬 더 좋은 방법입니다. 그래디언트의 반대 방향으로 가중치를 이동하면 손실이 감소됩니다.

2.4.1 변화율이란?

(1) 평균변화율

함수 y=f(x)에서 x의 값이 a에서 b까지 변할 때, 평균 변화율은 (f(x)의 변화량) / (x의 변화량) = (f(b) - f(a))/ (b-a) = (f(a) + x의 변화량) - f(a) / x의 변화량으로 정의됩니다.

그리고 f(x)의 변화량과 x의 변화량은 기호로 각각 Δf(x), Δx라는 기호로도 나타낼 수 있는데, 그렇게 위 식을 쓰면

Δf(x) / Δx = (f(b) - f(a))/ (b-a) = (f(a) + Δx) - f(a) / Δx

라고도 쓸 수 있습니다.

간단히 말해서 함수 f(x)에서 a에서 b까지의 기울기를 의미합니다.

간단한 exercise로 y=x^2그래프에서 x의 값이 1에서 2까지 변할 때 평균 변화율을 생각해 보면,

Δf(x) = 2^2 - 1^2 = 4 - 1 = 3

Δx = 2 - 1 = 1

즉, 평균 변화율 Δf(x) / Δx = 3/1 = 3 이 됩니다.

이는 (1,f(1))과 (2,f(2))를 잇는 직선의 기울기가 됩니다.

(2) 순간 변화율

순간 변화율이란, 평균 변화율에서 x의 변화량이 0에 수렴할 때의 값을 의미합니다.

lim(b-a -> 0) (f(b) - f(a)) / (b-a) = lim (Δx->0) Δf(x) / Δx = lim(Δx -> 0) (Δ(x) + Δf(x)) / Δ(x)

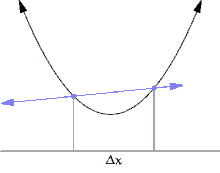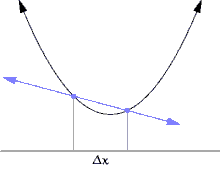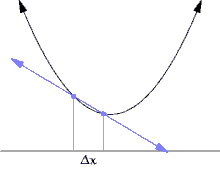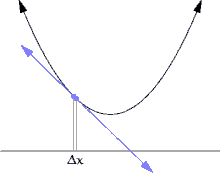
위의 그래프를 보며 이해해보겠습니다.

위의 그래프에서 왼쪽의 파란 점을 x, 오른쪽의 파란 점을 x+Δx라고 하겠습니다.

이 때, Δx의 값을 대략 한 10에서 0으로 쭉 쭉 줄여보면, Δx (x의 변화량)의 값도 0으로 쭉쭉 줄어들게 됩니다.

그리고 Δx를 계속해서 줄이면 x가 x에서 Δx까지 변할 때의 평균 변화율도 계속해서 변화합니다.

그러다가, Δx를 0에 수렴하게 줄이게 되면 저 두 점이 거의 만나게 될 것입니다. (실제로 만나는 것은 아닙니다. 극한값으로 가는것 뿐입니다.)

이때 나오는 순간 변화율의 값을 미분계수라고 하고, 이 미분계수를 찾는 과정을 바로 미분이라고 합니다.

그런데 저 그래프를 자세히 보면, 순간 변화율은 Δx가 0으로 수렴할 때의 평균 변화율이라고 했으므로 Δx가 0으로 수렴할 때, 파란 직선은 그래프의 접선으로 바뀌게 됩니다!

(3) 선형 근사

함수 f(x) = y는 연속성의 개념을 가집니다. 즉, x를 작은 값 epsilon_x만큼 증가시켰을 때 y가 epsilon_y만큼 바뀐다고 할 수 있습니다.

f(x + epsilon_x) = y + epsilon_y

epsilon_x가 충분히 작다면 어떤 포인트 p에서 기울기 a의 선형 함수로 f를 근사할 수 있습니다. 따라서 epsilon_y는 a * epsilon_x가 됩니다.

f(x + epsilon_x) = y + a * epsilon_x

이 선형적인 근사는 x가 p에 충분히 가까울 때 유효합니다.

위 기울기를 p에서 f의 변화율(derivative)이라고 합니다.

a가 음수일 때 p에서 양수 x만큼 조금 이동하면 f(x)가 감소한다는 것을 의미합니다.

a가 양수일 때 p에서 음수 x만큼 조금 이동하면 f(x)가 감소됩니다.

a의 절댓값(변화율의 크기)은 이런 증가나 감소가 얼마나 빠르게 일어날지 알려줍니다.

2.4.2 텐서 연산의 변화율: 그래디언트

그래디언트는 텐서 연산의 변화율입니다.

입력 벡터 x, 행렬 W, 타깃 y와 손실 함수 loss가 있다고 가정하겠습니다.

W를 사용하여 타깃의 예측 y_pred를 계산하고 손실, 즉 타깃 예측 y_pred와 타깃 y 사이의 오차를 계산할 수 있습니다.

y_pred = dot(W, t)
loss_value = loss(y_pred, y)

입력 데이터 x와 y가 고정되어 잇다면 이 함수는 W를 손실 값에 매핑하는 함수로 볼 수 있습니다.

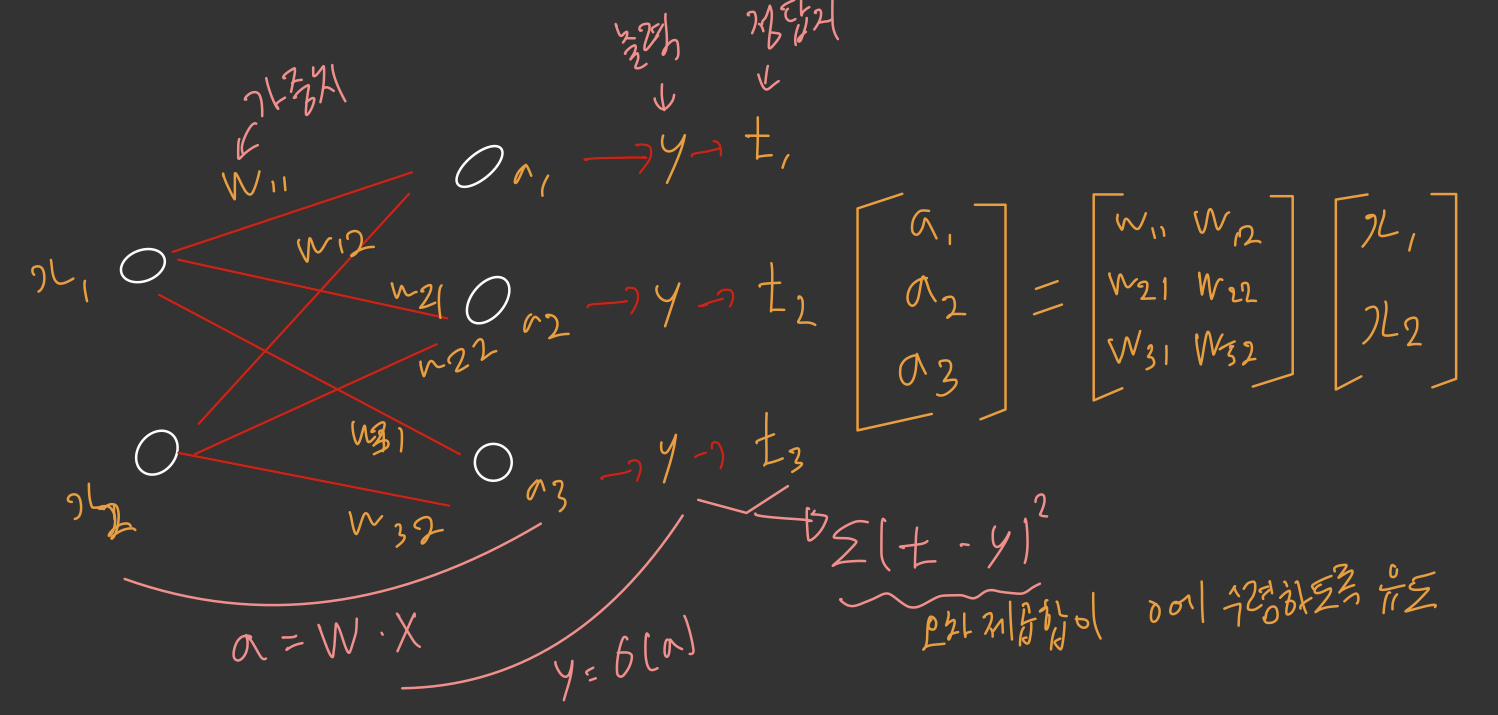
loss_value = f(W)

W의 현재 값을 W0라고 하겠습니다. 포인트 W0에서 f의 변화율은 W와 같은 크기의 텐서인 gradient(f)(W0)입니다. 이 텐서의 각 원소 gradient(f)(W0)[i, j]는 W0[i,j]를 변경했을 때 loss_value가 바뀌는 방향과 크기를 나타냅니다.

다시 말해 텐서 gradient(f)(W0)가 W0에서 함수 f(W) = loss_value의 그래디언트입니다.

gradient(f)(W0)는 W0에서 f(W)의 기울기를 나타내는 텐서로 해석할 수 있습니다.

그렇기 때문에 함수 f(x)에 대해서 변화율의 반대 방향으로 x를 움직이면 f(x)의 값을 감소시킬 수 있습니다. 동일하게 함수 f(W)의 입장에서는 그래디언트의 반대 방향으로 W를 움직이면 f(W)의 값을 줄일 수 있습니다.

예를 들어 W1 = W0 - step * gradient(f)(W0)가 있습니다.(step은 스케일을 조정하기 위한 작은 값입니다)

이는 기울기가 작아지는 곡면의 낮은 위치로 이동된다는 의미입니다. gradient(f)(W0)는 W0에 아주 가까이 있을 때 기울기를 근사한 것이므로 W0에서 너무 크게 벗어나지 않기 위해 스케일링 비율 step이 필요합니다.

2.4.3 확률적 경사 하강법

미분 가능한 함수가 주어지면 이론적으로 이 함수의 최솟값을 해석적으로 구할 수 있습니다. 함수의 최솟값은 변화율이 0인 지점입니다. 따라서 변화율이 0이되는 지점을 모두 찾고 이 중에서 어떤 포인트의 함수 값이 가장 작은지 확인하는 것입니다.

신경망에 적용하면 가장 작은 손실 함수의 값을 만드는 가중치의 조합을 해석적으로 찾는 것을 의미합니다. 이는 gradient(f)(W) = 0을 풀면 해결됩니다.

이 식은 N개의 변수로 이루어진 다항식으로 N은 네트워크의 가중치 개수를 뜻합니다.
N = 2나 N = 3인 식을 푸는 것은 가능하지만 실제 신경망에서는 파라미터의 개수가 종종 수천만 개가 되기 때문에 해석적으로 해결하는 것이 어렵습니다.

따라서 랜덤한 배치 데이터에서 현재 손실 값을 토대로 하여 조금씩 파라미터를 수정하여야 합니다. 미분 가능한 함수를 가지고 있으므로 gradient를 계산하여 단계 4를 효율적으로 구현할 수 있습니다. gradient의 반대 방향으로 가중치를 업데이트하면 손실이 매번 조금씩 감소할 것입니다.

미니 배치 확률적 경사 하강법(mini-batch SGD)

1. 훈련 샘플 배치 x와 이에 상응하는 target y를 추출합니다.
2. x로 네트워크를 실행하고 예측 y_pred를 구합니다.
3. 이 배치에서 y_pred와 y 사이의 오차를 측정하여 네트워크의 손실을 계산합니다.
4. 네트워크의 파라미터에 대한 손실 함수의 gradient를 계산합니다(역방향 패스(backwardpass)).
5. gradient의 반대 방향으로 parameter를 조금 이동시킵니다. 예를 들어 W -= step * gradient처럼 하면 배치에 대한 손실이 조금 감소할 것입니다.

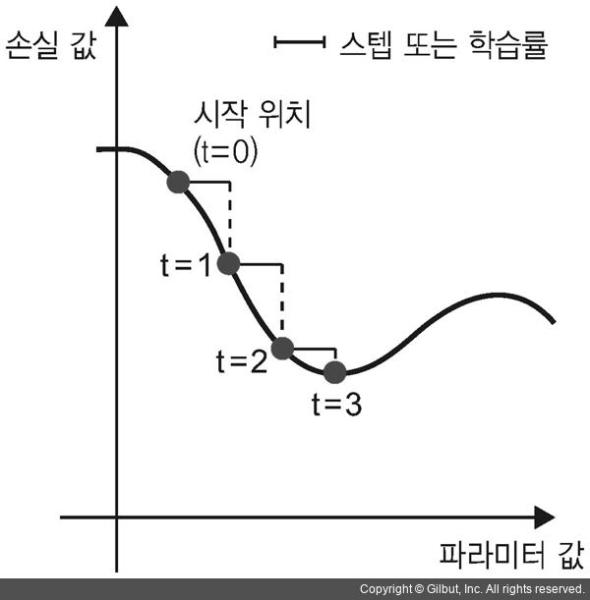
SGD가 1D 손실 함수(1개의 학습 파라미터)의 값을 낮춰줍니다.

그림에서 볼 수 있듯이 step 값을 적절히 고르는 것이 중요합니다. 값이 너무 작으면 곡선을 따라 내려가는데 너무 많은 반복이 필요하고 지역 최솟값(local minimum)에 갇힐 수 있습니다. step이 너무 크면 손실 함수 곡선에서 완전히 임의의 위치로 이동시킬 수 있습니다.

적절한 크기의 미니 배치를 사용하는 것이 중요합니다.

또 업데이트할 다음 가중치를 계산할 때 현재 gradient 값만 보지 않고 이전에 업데이트된 가중치를 여러 가지 다른 방식으로 고려하는 SGD 변종이 많이 있습니다. 예를 들어 모멘텀을 사용한 SGD, Adagrad, RMSProp 등입니다. 이런 변종들을 모두 최적화 방법(optimization method) 또는 옵티마이저라고 부릅니다. 특히 여러 변종들에서 사용하는 모멘텀(momentum) 개념은 아주 중요합니다.

모멘텀은 경사하강법을 통해 W가 이동하는 과정에서 일종의 ‘관성’을 부여하는 것입니다. 즉 W를 업데이트 할 때에 이전 단계의 업데이트 방향을 반영하는 것입니다.

모멘텀은 SGD에 있는 2개의 문제점인 수렴 속도와 지역 최솟값을 해결합니다. 아래 그림은 네트워크의 하나에 대한 손실 값의 곡선을 보여 줍니다.

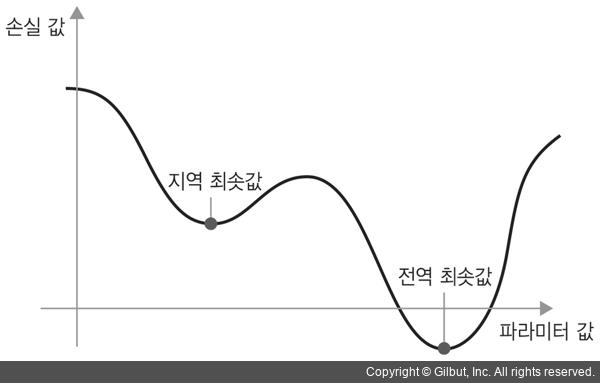위 그림과 같이 어떤 파라미터 값에서는 지역 최솟값에 도달합니다. 그 지점 근처에서는 왼쪽으로 이동해도 손실이 증가하고, 오른쪽으로 이동해도 손실이 증가합니다.

대상 파라미터가 작은 학습률을 가진 SGD로 최적화되었다면 최적화 과정이 전역 최솟값으로 향하지 못하고 이 지역 최솟값에 갇히게 될 것입니다.

여기에서 모멘텀이 충분하면 지역 최솟값에 갇히지 않고 전역 최솟값에 도달할 수 있습니다. 모멘텀은 현재 gradient 값 뿐만 아니라 이전에 업데이트한 파라미터에 기초하여 파라미터 w를 업데이트합니다.

past_velocity = 0.
momentum = 0.1 # 모멘텀 상수
while loss > 0.01: # 최적화 반복 루프
    w, loss, gradient = get_current_parameters()
    velocity = momentum * past_velocity - learning_rate * gradient
    w = w + momentum * velocity - learning_rate * gradient
    past_velocity = velocity
    update_parameter(w)

다시 한 번 gradient descent를 정리해보겠습니다.

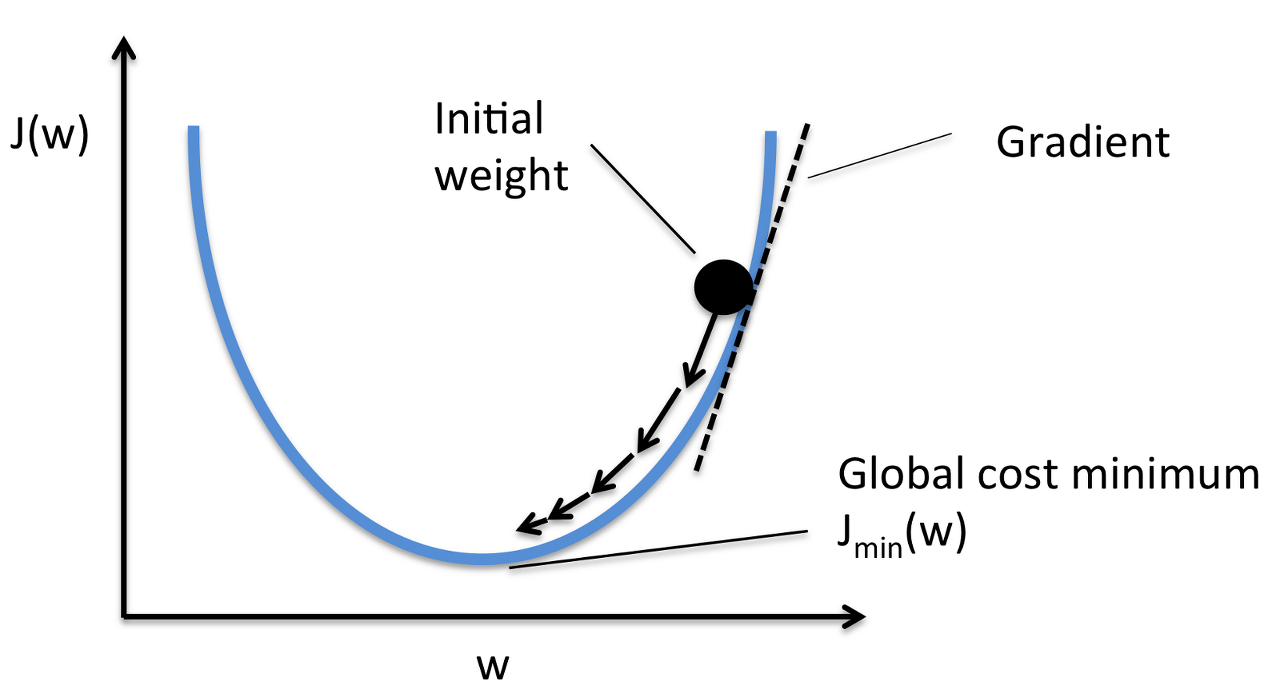
Gradient Descent에서 어떤 함수 f(x)가 최소가 되는 x를 찾는 것이 목표입니다.

위의 경우에는 x축에 w, y축에 J(w)로 적혀 있으므로 이를 따라 J(w)가 최소가 되는 w의 값을 찾아야합니다.

만약 처음 w값이 위의 그래프처럼 오른쪽 위쯤에 있다고 가정하겠습니다.

그러면 그 W값을 미분하면, 위처럼 양수의 미분계수가 나오게 됩니다.

미분계수가 양수라면, 즉 접선의 기울기가 왼쪽 아래와 오른쪽 위를 향하고 있다면 어떤 부분의 함숫값이 더 작을까요?

접선이 왼쪽 아래와 오른쪽 위를 향하고 있으므로, 당연히 아래를 향하는 왼쪽 부분의 함숫값이 더 작을 것입니다.

그리고 Gradient Descent의 목표는 J(w)가 최소가 되는 w의 값을 찾는 것이므로, w를 함숫값이 더 작은 왼쪽 부분으로 넘겨 주어야 합니다.

즉, 어떤 함수에서 w값에 대한 미분계수가 양수라면, w의 값을 줄여주어야 합니다.

그렇다면 반대로 처음 w값이 왼쪽에 있었다면 어땠을까요?

그럼 x=w에서의 미분계수는 음수가 되었을 것입니다. 그리고 이 때는 접선의 기울기가 왼쪽 위와 오른쪽 아래를 향하고 있으므로, 함숫값은 왼쪽보다 오른쪽이 더 낮을 것입니다.

그리고 우리의 목적은 함숫값 J(w)를 최소로 하는 w의 값을 찾는 것이므로, w를 함숫값이 더 작은 오른쪽 부분으로 넘겨 주어야 합니다. 즉, w의 값을 더 늘려야 하는 것이죠.

따라서 어떤 함수에서 w값에 대한 미분계수가 음수라면, w의 값을 늘려주어야 합니다.

마지막으로 위에서 정리한 두개의 사실들을 하나로 합치자면, “w의 값을 미분계수의 부호의 반대쪽으로 옮겨야 한다”입니다!

즉, 미분계수가 양수라면 w를 줄여야하고, 미분계수가 음수라면 w를 늘려야한다는 것입니다.

(∂/∂W cost(W)는 cost(W)를 W에 대해 미분한다는 뜻입니다.)

양수를 빼면 줄어들고, 음수를 빼면 늘어나기 때문에, 저 미분계수에다가 α를 곱한 값을 w에서 빼주면 된다는 것입니다!

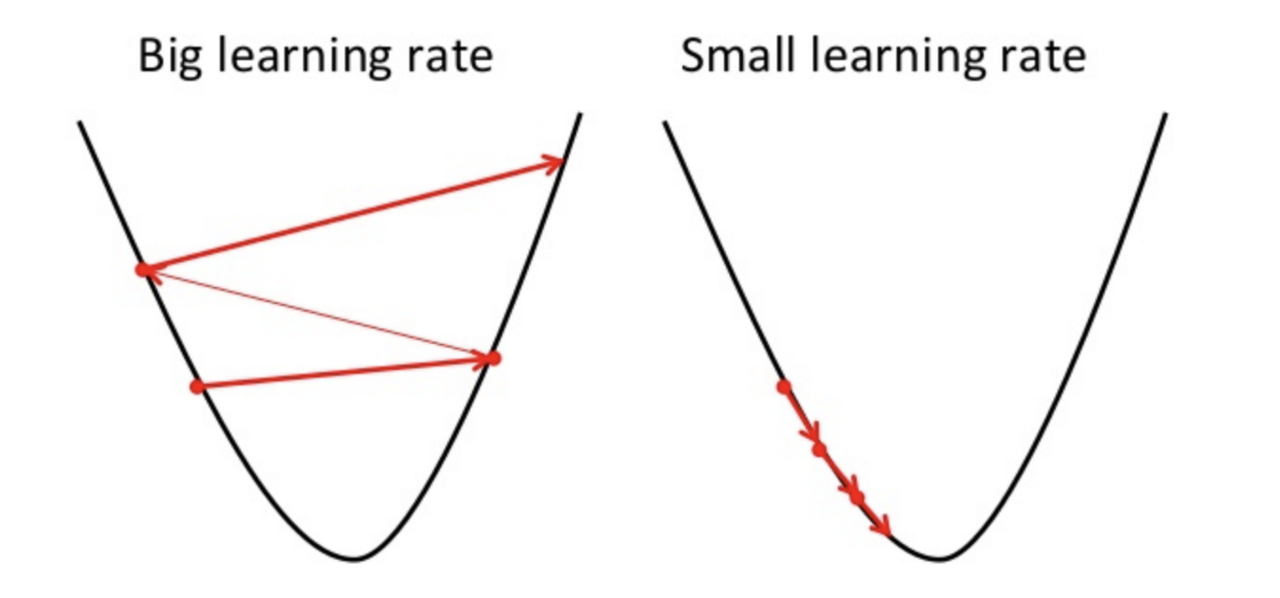
α를 곱하는 이유는 미분계수에다가 α를 곱하지 않으면 w의 값을 한 번에 너무 멀리 보내버리게 되기 때문입니다.

그러면 위의 그림에서 왼쪽의 그래프마냥, J(w)값이 줄어들기는 커녕 늘어나는 방향으로 w가 바뀔 수도 있습니다.

그리고 마냥 미분계수만큼만 빼버리면 웬만하면 저런 식으로 w값이 날라가게 되므로, α값을 곱해주어 너무 멀리 가는 것을 방지해 주는 것입니다. (일반적으로 α는 1보다는 작고 0보다는 큰 값입니다. 참고로, α는 learning rate라고 불립니다.)

이러한 이유에서, Gradient Descent를 반복하면, 즉! W := W - α * ∂/∂W * cost(W)를 반복하면, 결국 w의 값이 J(w)가 최소가 되는 값으로 수렴하게 된다는 것을 알 수 있습니다!

2.4.4 변화율 연결: 역전파 알고리즘

3개의 텐서 연산 a, b, c와 가중치 행렬 W1, W2, W3로 구성된 네트워크 f를 예로 들어 보겠습니다.

f(W1, W2, W3) = a(W1, b(W2, c(W3)))

미적분에서 이렇게 연결된 함수는 연쇄 법칙(chain rule)이라 부르는 다음의 항등식 `f(g(x))’ = f’(g(x)) * g’(x)를 사용하여 유도될 수 있습니다.

연쇄 법칙을 신경망의 gradient 계산에 적용하여 역전파(Backpropagation) 알고리즘(후진 모드 자동 미분(reverse-mode automatic differentiation)이라고도 부릅니다)이 탄생되었습니다.

2.5 첫 번째 예제 다시 살펴보기

먼저 입력 데이터입니다.

(train_images, train_labels), (test_images, test_labels) = mnist.load_data()

train_images = train_images.reshape((60000, 28 * 28))
train_images = train_images.astype('float32') / 255

test_images = test_images.reshape((10000, 28*28))
test_images = test_images.astype('float32') / 255

입력 이미지의 데이터 타입은 float32로, 훈련 데이터는 (60000, 784) 크기, 테스트 데이터는 (10000,784) 크기의 numpy array로 저장됩니다.

우리가 사용할 신경망입니다.

network = models.Sequential()
network.add(layers.Dense(512, activation='relu', input_shape=(28*28, )))
network.add(layers.Dense(10, activation='softmax'))

이 네트워크는 2개의 Dense 층이 연결되어 있고 각 층은 가중치 텐서를 포함하여 입력 데이터에 대한 몇 개의 간단한 텐서 연산을 적용합니다. 층의 속성인 가중치 텐서는 네트워크가 정보를 저장하는 곳입니다.

이제 네트워크를 컴파일하는 단계입니다.

network.compile(optimizer = 'rmsprop',
                loss = 'categorical_crossentropy',
                metrics=['accuracy'])

categorical_crossentropy는 손실 함수입니다. 가중치 텐서를 학습하기 위한 피드백 신호로 사용되며 훈련하는 동안 최소화됩니다. 미니 배치 확률적 경사 하강법을 통해 손실이 감소됩니다. 경사 하강법을 적용하는 구체적인 방식은 첫 번째 매개변수로 전달된 rmsprop 옵티마이저에 의해 결정됩니다.

마지막으로 훈련 반복입니다.

network.fit(train_images, train_labels, epochs = 5, batch_size = 128)

fit 메서드를 호출하면 네트워크가 128개 샘플씩 미니 배치로 훈련 데이터를 다섯 번 반복합니다(전체 훈련 데이터에 수행되는 각 반복을 에포크(epoch) 라고 합니다). 각 반복마다 네트워크가 배치에서 손실에 대한 가중치의 그래디언트를 계산하고 그에 맞추어 가중치를 업데이트합니다.

다섯 번의 에포크 동안 네트워크는 2,345번의 gradient update를 수행할 것입니다(에포크마다 469번).

훈련 샘플이 6만 개이므로 128개씩 배치로 나누면 469개의 배치가 만들어지며 마지막 배치의 샘플 개수는 96개가 됩니다.

2.6 요약

마지막으로 chapter 02장을 정리하겠습니다.

• 학습(Learning)은 훈련 데이터 샘플과 그에 상응하는 target이 주어졌을 때 손실 함수를 최소화하는 모델 파라미터의 조합을 찾는 것을 의미합니다.

• 데이터 샘플과 타깃의 배치를 랜덤하게 뽑고 이 배치에서 손실에 대한 파라미터의 그래디언트를 계산함으로써 학습이 진행됩니다. 네트워크의 파라미터는 그래디언트의 반대 방향으로 조금씩(학습률에 의해 정의된 크기만큼) 움직입니다.

• 전체 학습 과정은 신경망이 미분 가능한 텐서 연산으로 연결되어 있기 때문에 가능합니다. 현재 파라미터와 배치 데이터를 그래디언트 값에 매핑해 주는 그래디언트 함수를 구성하기 위해 미분의 연쇄 법칙을 사용합니다.

• 손실과 옵티마이저는 네트워크에 데이터를 주입하기 전에 정의되어야 합니다.

• 손실은 훈련하는 동안 최소화해야 할 양이므로 해결하려는 문제의 성공을 측정하는데 사용합니다.

• 옵티마이저는 손실에 대한 그래디언트가 파라미터를 업데이트하는 정확한 방식을 정의합니다. Ex) RMSProp 옵티마이저, 모멘텀을 사용한 SGD etc..

Reference

1. 케라스 창시자에게 배우는 딥러닝
2. https://cding.tistory.com/56