[DeepLearning] CH02. 신경망의 수학적 구성 요소(3)

in Deep Learning on Deeplearning


케라스 창시자에게 배우는 딥러닝을 기반으로 공부한 내용을 정리합니다.

2.3 신경망의 톱니바퀴: 텐서 연산

keras.layers.Dense(512, activation='relu') 이 층은 2D 텐서를 입력으로 받고 입력 텐서의 새로운 표현인 또 다른 2D 텐서를 반환하는 함수처럼 해석할 수 있습니다. W는 2D 텐서고, b는 벡터입니다. 둘 모두 층의 속성입니다.

output = relu(dot(W, input) + b) 입력 텐서와 텐서 W사이의 점곱(dot), 점곱의 결과인 2D 텐서와 벡터 b 사이의 덧셈(+), 마지막으로 relu 연산으로 3개의 텐서 연산이 있습니다.
relu(x)는 max(x, 0)입니다. <- 입력 값이 0보다 크면 x값 그대로, 0보다 작으면 x값은 0으로 출력됩니다.

2.3.1 원소별 연산

relu 함수와 덧셈은 원소별 연산(element-wise operation)입니다. 이 연산은 텐서에 있는 각 원소에 독립적으로 적용됩니다.

relu 연산 구현

def naive_relu(x):
    assert len(x.shape) == 2 # 2D가 아니면 error 발생

    x = x.copy() # 입력 텐서 자체를 바꾸지 않도록 복사
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            x[i, j] = max(x[i, j], 0)
    return x

덧셈 연산 구현

def naive_add(x, y):
    assert len(x.shape) == 2
    assert x.shape == y.shape

    x = x.copy()
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            x[i, j] += y[i, j]
    return x

2.3.2 브로드캐스팅

작은 텐서가 큰 텐서의 크기에 맞추어 브로드캐스팅(broadcasting)됩니다.

  1. 큰 텐서의 ndim에 맞도록 작은 텐서에 (브로드캐스팅 축이라고 부르는) 축이 추가됩니다.
  2. 작은 텐서가 새 축을 따라서 큰 텐서의 크기에 맞도록 반복됩니다.

예를 들어 설명해보겠습니다.
x의 크기는 (32, 10)이고 y의 크기는 (10, )라고 가정합시다. 먼저 y에 비어 있는 첫 번째 축을 추가하여 크기를 (1, 10)으로 만듭니다. 그런 다음 y를 이 축에 32번 반복하면 텐서 y의 크기는 (32, 10)이 됩니다.

브로드 캐스팅 구현

def naive_add_matrix_and_vector(x, y):
    assert len(x.shape) == 2 # x는 2D numpy array
    assert len(y.shape) == 1 # y는 numpy vector
    assert x.shape[1] == y.shape[0]

    x = x.copy()
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            x[i, j] += y[j] # broadcasting
    return x

다음은 크기가 다른 두 텐서에 브로드캐스팅으로 원소별 maximum 연산을 적용하는 예입니다.

import numpy as np

x = np.random.random((64, 3, 32, 10))
y = np.random.random((32, 10))

z = np.maximum(x, y) # 출력 z 크기는 x와 동일하게 (64, 3, 32, 10)입니다.

2.3.3 텐서 점곱(점곱 연산, dot operation)

원소별 곱셈은 * 연산자를 사용합니다.
점곱 연산은 dot 연산자를 사용합니다.

점곱 연산 수행

def naive_vector_dot(x, y):
    assert len(x.shape) == 1 # numpy vector
    assert len(y.shape) == 1
    assert x.shape[0] == y.shape[0]

    z = 0.
    for i in range(x.shape[0]):
        z += x[i] * y[i]
    return z

두 벡터의 점곱은 스칼라가 되므로 원소 개수가 같은 벡터끼리 점곱이 가능합니다.

행렬 x와 벡터 y 사이에서도 점곱이 가능합니다.

import numpy as np
def naive_matrix_vector_dot(x,y):
    assert len(x.shape) == 2
    assert len(y.shape) == 1
    assert x.shape[1] == y.shape[0] # x의 두 번째 차원 == y의 첫 번째 차원

    z = np.zeros(x.shape[0]) # x의 행과 같은 크기의 0이 채워진 벡터를 만듭니다.
    for i in range(x.shape[0]):
        for j in range(x.shape[1]):
            z[i] += x[i, j] * y[j]
    return z

만약 두 텐서 중 하나라도 ndim이 1보다 크면 dot 연산에 교환 법칙이 성립되지 않습니다.
즉 dot(x, y)와 dot(y, x)가 같지 않다는 것을 뜻합니다. 따라서 x.shape[1] == y.shape[0]일 때 두 행렬 x와 y의 점곱(dot(x, y))이 성립됩니다.

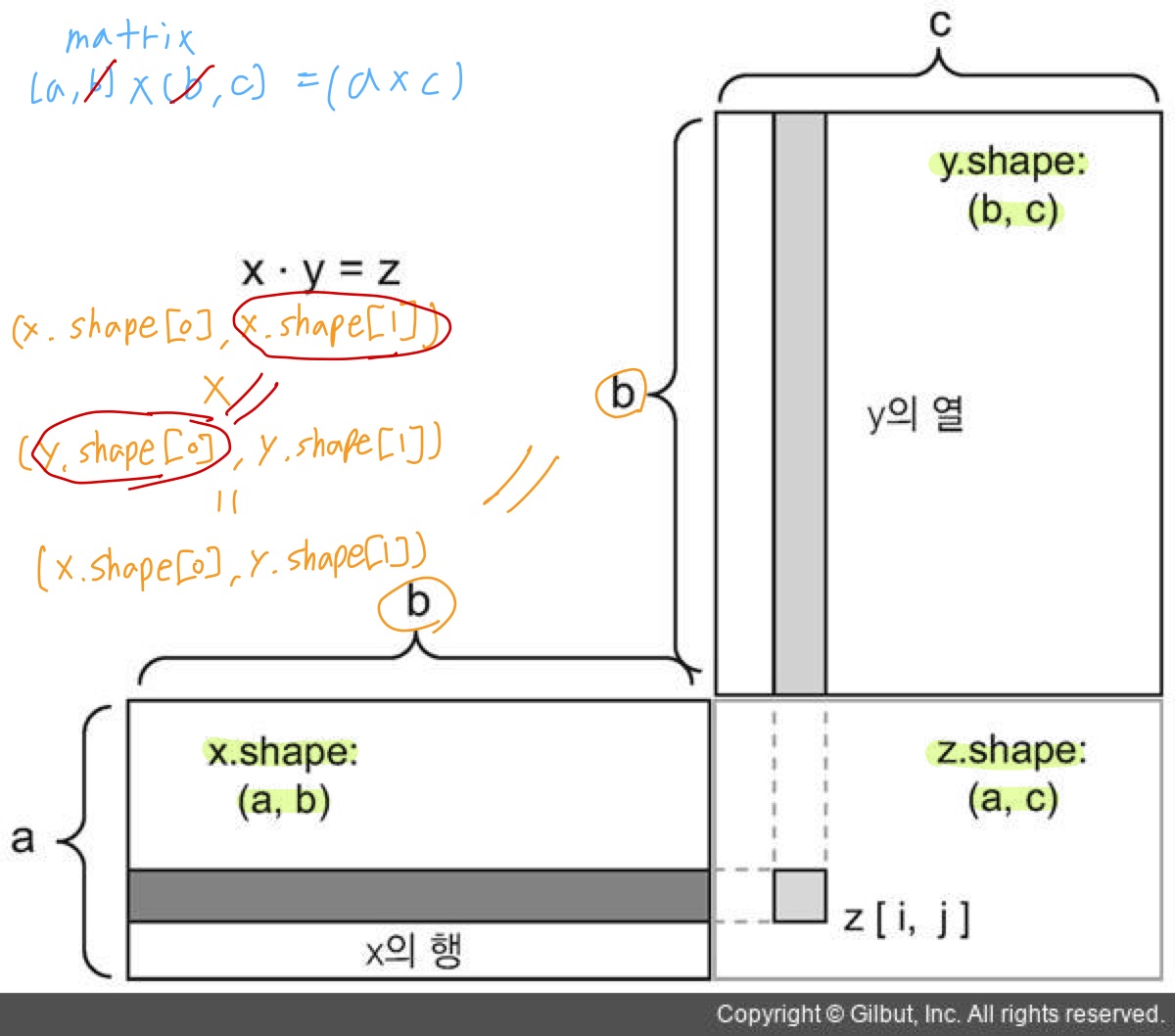
x의 행과 y의 열 사이 벡터 점곱으로 인해 (x.shape[0], y.shape[1])크기의 행렬이 됩니다.

def naive_matrix_dot(x, y):
    assert len(x.shape) == 2
    assert len(y.shape) == 2
    assert x.shape[1] == y.shape[0] # matrix 연산 a * b = b * c = a * c
    
    z = np.zeros((x.shape[0], y.shape[1]))
    for i in range(x.shape[0]):
        for j in range(y.shape[1]):
            row_x = x[i, :]
            column_y = y[:, j]
            z[i, j] = naive_vector_dot(row_x, column_y)
    return z

img

2.3.4 텐서 크기 변환(tensor reshaping)

신경망에 주입할 숫자 데이터를 전처리할 때 사용할 수 있습니다.

train_images = train_images.reshape((60000, 28 * 28))
텐서의 크기를 변환한다는 것은 특정 크기에 맞게 열과 행을 재배열한다는 뜻입니다. 당연히 크기가 변환된 텐서는 원래 텐서와 원소 개수가 동일합니다.

x = np.array([[0., 1.],
                [2., 3.],
                [4., 5.]])
>>> print(x.shape)
(3,2)

x = x.reshape((6, 1))
>>> x
array([[0.],
       [1.],
       [2.],
       [3.],
       [4.],
       [5.]])
x = x.reshape((2, 3))
>>> x
array([[ 0., 1., 2.],
       [ 3., 4., 5.]])

전치(transposition)는 행과 열을 바꾸는 것입니다. 

x = np.zeros((300, 20))
x = np.transpose(x)
>>> print(x.shape)
(20, 300)

2.3.5 텐서 연산의 기하학적 해석

텐서 연산이 조작하는 텐서의 내용은 어떤 기하학적 공간에 있는 좌표 포인트로 해석될 수 있기 때문에 모든 텐서 연산은 기하학적 해석이 가능합니다.

A = [0.5, 1]
이 포인트는 2D 공간에 있습니다. 여기에 새로운 포인트 B = [1, 0.25]를 A 벡터에 더해 보겠습니다. 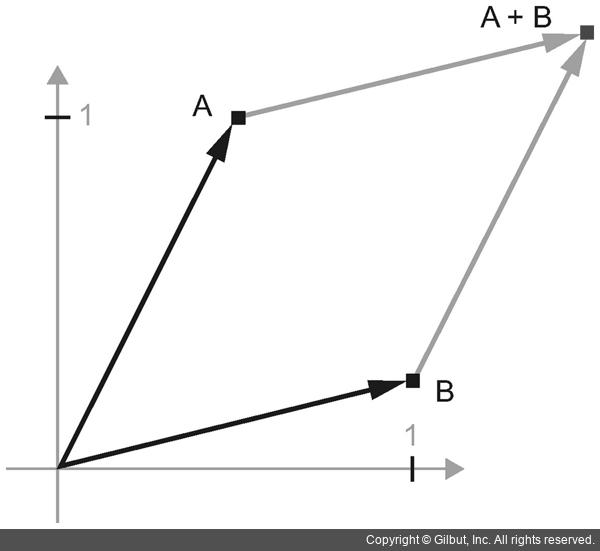img 두 벡터의 덧셈에 대한 기하학적 해석

2.3.6 딥러닝의 기하학적 해석

신경망은 전체적으로 텐서 연산의 연결로 구성된 것이고, 모든 텐서 연산은 입력 데이터의 기하학적 변환임을 배웠습니다. 단순한 단계들이 길게 이어져 구현된 신경망을 고차원 공간에서 매우 복잡한 기하학적 변환을 하는 것으로 해석할 수 있습니다.



Reference

  1. 케라스 창시자에게 배우는 딥러닝



© 2020. by GeonKimdcu

Powered by aiden